
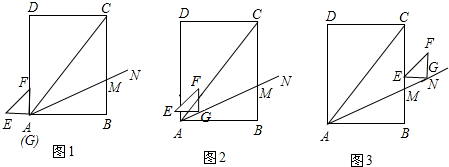
分析 (1)三角形一个角的平分线,这个角平分线其对边所成的两条线段与这个角的两邻边对应成比例,所以$\frac{BM}{CM}$=$\frac{AB}{AC}$,先由勾股定理求出AC的值后,然后将相关线段的长代入比例式中即可求出BM的值;由FG∥BC得△AFG∽△AMC,列比例式代入即可求出时间t的值;
(2)先根据题意求出路程AG=$\sqrt{5}$t,及△GEF的面积,分四种情况进行讨论:①当0≤t≤$\frac{6}{5}$时,此时,△GEF和△ACM重叠的部分为△PGH,利用比例式求出PG和GH,利用面积公式求出结论;②当$\frac{6}{5}$<t≤$\frac{8}{5}$时,此时,△GEF和△ACM重叠的部分为四边形,利用△GEF的面积减去小三角形面积来求;③当$\frac{8}{5}$<t≤3时,如图4,S=S△EGF=2;④当3<t≤4时,如图5,△GEF和△ACM重叠的部分为△EPH,同理可得;
(3)分三种情况进行讨论:①当CP=CQ时,设CP=x,过P作PH⊥BC于H,利用相似求QG的长,再利用勾股定理求列方程求出x的值;②当CP=PQ时,同理可得出CP的长;③当CQ=PQ时,作辅助线构建相似三角形,利用比例式求QG的长,同理列方程求CP;最后写出结论.
解答 解:(1)在Rt△ABC中,
∴AC2=AB2+BC2,
∴AC=10,
∵∠BAC的角平分线AN交BC于点M,
∴$\frac{AB}{AC}=\frac{BM}{CM}$,
∴$\frac{BM}{CM}$=$\frac{3}{5}$,
∵BC=8,
∴BM=3,CM=5
∴由勾股定理可得:AM=3$\sqrt{5}$,
当F在AC上时,如图1,
此时FG∥BC,
∴△AFG∽△AMC
∴$\frac{GF}{CM}=\frac{AG}{AM}$,
∴$\frac{2}{5}$=$\frac{\sqrt{5}t}{3\sqrt{5}}$,
∴t=$\frac{6}{5}$;
故答案为:3,$\frac{6}{5}$;
(2)由题意知:AG=$\sqrt{5}$t,
△GEF的面积为:$\frac{1}{2}$GE•GF=2
当E在AC上时,此时t=$\frac{8}{5}$,
①当0≤t≤$\frac{6}{5}$时,如图2,此时,△GEF和△ACM重叠的部分为△PGH,
过M作MQ∥AB,交AC于Q,
∴$\frac{QM}{AB}=\frac{CM}{BC}$,
∴$\frac{QM}{6}=\frac{5}{8}$,则QM=$\frac{15}{4}$,
∵GH∥MQ,
∴$\frac{GH}{MQ}=\frac{AG}{AM}$,
∴$\frac{GH}{\frac{15}{4}}=\frac{\sqrt{5}t}{3\sqrt{5}}$,
∴GH=$\frac{5t}{4}$,
同理得:$\frac{PG}{5}=\frac{\sqrt{5}t}{3\sqrt{5}}$,PG=$\frac{5t}{3}$,
∴S=S△PGH=$\frac{1}{2}$×HG×PG=$\frac{1}{2}$×$\frac{5t}{4}$×$\frac{5t}{3}$=$\frac{25}{24}$t2;
②当$\frac{6}{5}$<t≤$\frac{8}{5}$时,如图3,
此时,△GEF和△ACM重叠的部分为四边形,
设EF与AC交于点P,过P作PQ⊥EG于Q,EG与AC交于H,
GH=$\frac{5t}{4}$,EH=2-$\frac{5t}{4}$,
∵EG∥AB,
∴tan∠CAB=tan∠PHG=$\frac{8}{6}$=$\frac{4}{3}$,
设PQ=4x,HQ=3x,则EH=4x-3x=x,
∴PQ=4(2-$\frac{5t}{4}$),
∴S=S四边形PHGF=S△EGF-S△PEH=2-$\frac{1}{2}$×EH×PQ=2-$\frac{1}{2}$×(2-$\frac{5t}{4}$)•4(2-$\frac{5t}{4}$),
则S=-$\frac{25}{8}$t2+10t-6;
③当$\frac{8}{5}$<t≤3时,如图4,S=S△EGF=2;
④当3<t≤4时,如图5,△GEF和△ACM重叠的部分为△EPH,
∵EG∥AB,
∴△PMG∽△BMA,
∴$\frac{PG}{AB}=\frac{MG}{AM}$,
∴$\frac{PG}{6}=\frac{\sqrt{5}t-3\sqrt{5}}{3\sqrt{5}}$,
∴PG=2t-6,
∴S=S△PEF=$\frac{1}{2}$×PE×PH=$\frac{1}{2}$(2t-6)2=2t2-16t+32;
(3)分三种情况:①当CP=CQ时,如图6,
设CP=x,则CQ=x,EQ=4-x,
过P作PH⊥BC于H,
则PH=$\frac{3x}{5}$,CH=$\frac{4x}{5}$,HQ=x-$\frac{4x}{5}$=$\frac{x}{5}$,
∵△PHQ∽△EGQ,
∴$\frac{PH}{EG}=\frac{HQ}{QG}$,
∴$\frac{\frac{3x}{5}}{2}=\frac{\frac{x}{5}}{QG}$,
∴QG=$\frac{2}{3}$,
由勾股定理得:EG2=QG2+EG2,
(4-x)2=$(\frac{2}{3})^{2}$+22,
(4-x)2=$\frac{40}{9}$,
x=4±$\frac{2\sqrt{10}}{3}$,
∴CP=4±$\frac{2\sqrt{10}}{3}$;
②当CP=PQ时,如图7,过P作PH⊥BC于H,
设CH=x,则HQ=x,EQ=4-2x,PH=$\frac{3x}{4}$,PC=$\frac{5x}{4}$,
∵△FHQ∽△EGQ,
∴$\frac{PH}{EG}=\frac{HQ}{QG}$,
∴$\frac{\frac{3x}{4}}{2}=\frac{x}{QG}$,
∴QG=$\frac{8}{3}$,
∴(4-2x)2=$(\frac{8}{3})^{2}$+22,
(4-2x)2=$\frac{100}{9}$,
x1=$\frac{11}{3}$,x2=$\frac{1}{3}$,
∴PC=$\frac{55}{12}$或$\frac{5}{12}$;
③当CQ=PQ时,如图8,过P作过P作PH⊥BC于H, 过Q作QT⊥AC于T,
过Q作QT⊥AC于T,
设CP=x,则CQ=$\frac{5}{8}$x,PH=$\frac{3x}{5}$,QE=4-$\frac{5}{8}$x,
∵△PHQ∽△EGQ,
∴$\frac{PH}{EG}=\frac{HQ}{GQ}$,
∴$\frac{\frac{3x}{5}}{2}=\frac{\frac{4x}{5}-\frac{5x}{8}}{GQ}$,
∴GQ=$\frac{7}{12}$,
∴22+$(\frac{7}{12})^{2}$=(4-$\frac{5x}{8}$)2,
(4-$\frac{5x}{8}$)2=$\frac{625}{144}$,
x1=$\frac{146}{15}$,x2=$\frac{46}{15}$,
∴CP=$\frac{146}{15}$或$\frac{46}{15}$;
综上所述:PC=4±$\frac{2\sqrt{10}}{4}$或$\frac{5}{12}$或$\frac{55}{12}$或$\frac{46}{15}$或$\frac{146}{15}$.
点评 本题是四边形和二次函数的综合题,考查了相似三角形的性质和判定,考查了勾股定理及等腰三角形的性质,综合性较强;尤其是第(2)、(3)需要分多种情况进行讨论,容易出错,图形也比较多,本题的关键是能正确画出各种情况的图形.


科目:初中数学 来源:2016-2017学年山东省淄博市(五四学制)七年级下学期第一次月考数学试卷(解析版) 题型:单选题
如图,下列条件中:(1)∠B+∠BCD=180°;(2)∠1=∠2; (3)∠3=∠4;(4)∠B=∠5;能判定AB//CD的条件个数有( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省东台市第六教育联盟七年级下学期第一次月考数学试卷 题型:单选题
如图,下列判断正确的是:( )

A. 若∠1=∠2,则AD∥BC B. 若∠1=∠2,则AB∥CD
C. 若∠A=∠3,则AD∥BC D. 若∠3+∠DAB=180° ,则AB∥CD
查看答案和解析>>
科目:初中数学 来源:2016-2017学年广东省七年级下学期第一次月考数学试卷(解析版) 题型:单选题
 是一个完全平方式,则a的值为( )
是一个完全平方式,则a的值为( )
A. 4 B. 8 C. 4或-4 D. 8或-8
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
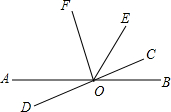 如图.直线AB与CD相交于点O,OF⊥OC,∠BOC:∠BOE=1:3,∠AOF=2∠COE
如图.直线AB与CD相交于点O,OF⊥OC,∠BOC:∠BOE=1:3,∠AOF=2∠COE查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 数学活动课,老师和同学一起去测量校内某处的大树AB的高度,如图,老师测得大树前斜坡DE的坡度i=1:4,一学生站在离斜坡顶端E的水平距离DF为8m处的D点,测得大树顶端A的仰角为α,已知sinα=$\frac{3}{5}$,BE=1.6m,此学生身高CD=1.6m,则大树高度AB为( )m.
数学活动课,老师和同学一起去测量校内某处的大树AB的高度,如图,老师测得大树前斜坡DE的坡度i=1:4,一学生站在离斜坡顶端E的水平距离DF为8m处的D点,测得大树顶端A的仰角为α,已知sinα=$\frac{3}{5}$,BE=1.6m,此学生身高CD=1.6m,则大树高度AB为( )m.| A. | 7.4 | B. | 7.2 | C. | 7 | D. | 6.8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com