
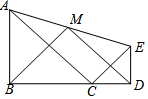
 如图,△ABC和△CDE均为等腰直角三角形,点B、C、D在一条直线上,点M是AE的中点,
如图,△ABC和△CDE均为等腰直角三角形,点B、C、D在一条直线上,点M是AE的中点,分析 (1)通过作辅助线MN,构建直角梯形的中位线,根据梯形的中位线定理及等腰直角三角形的判定定理解答即可;
(2)由三角形的面积公式、梯形的面积公式及不等式的基本性质a2+b2≥2ab(a=b时取等号)解答即可.
解答 解:(1)过点M作MN垂直于BD,垂足为N.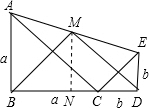
∵点M是AE的中点,
则MN为梯形中位线,
∴N为中点,
∴△BMD为等腰三角形,
∴BM=DM,
又∵MN=$\frac{1}{2}$(AB+ED)=$\frac{1}{2}$BC+CD),
∴∠BMD=90°,
即BM⊥DM.
(2)∵S△ABC=$\frac{1}{2}$a2,S△CDE=$\frac{1}{2}$b2,S梯形ABDE=$\frac{1}{2}$(a+b)2,
∴S△ACE=S梯形ABDE-S△ABC-S△CDE=ab,
S△ABC+S△CDE=$\frac{1}{2}$(a2+b2)≥ab(a=b时取等号),
∴S△ABC+S△CDE≥S△ACE.
点评 本题综合考查了等腰直角三角形的判定与性质、梯形的中位线定理,特别是不等式的基本性质a2+b2≥2ab(a=b时取等号)是解决问题的关键.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:选择题
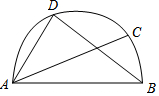 如图,AB是半圆的直径,∠BAC=20°,D是$\widehat{AC}$的中点,则∠DAC的度数是( )
如图,AB是半圆的直径,∠BAC=20°,D是$\widehat{AC}$的中点,则∠DAC的度数是( )| A. | 30° | B. | 35° | C. | 45° | D. | 70° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
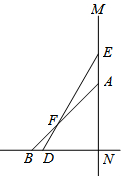 如图,一根6米长的竹竿DE斜靠的竖直的墙MN上,与地面所成的角∠EDN=60°,如果竹竿的顶端沿墙面下滑一段距离后竹竿与地面所成的角∠ABN=45°.
如图,一根6米长的竹竿DE斜靠的竖直的墙MN上,与地面所成的角∠EDN=60°,如果竹竿的顶端沿墙面下滑一段距离后竹竿与地面所成的角∠ABN=45°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
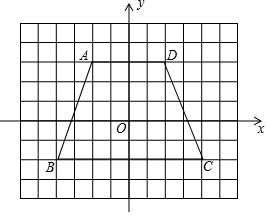 (1)写出如图所示的四边形ABCD各顶点的坐标.
(1)写出如图所示的四边形ABCD各顶点的坐标.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com