
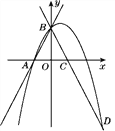
【题目】如图,直线y=2x+2与x轴交于点A,与y轴交于点B,把△AOB沿y轴翻折,点A落到点C,过点B的抛物线y=-x2+bx+c与直线BC交于点D(3,-4)
(1)求直线BD和抛物线对应的函数解析式;
(2)在抛物线对称轴上求一点P的坐标,使△ABP的周长最小;
(3)在第一象限内的抛物线上,是否存在一点M,作MN垂直于x轴,垂足为点N,使得以M,O,N为顶点的三角形与△BOC相似?若存在,求出点M的坐标;若不存在,请说明理由.
【答案】(1)y=-2x+2,y=-x2+x+2;(2)(![]() );(3)存在,M(1,2)或
);(3)存在,M(1,2)或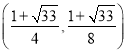 .
.
【解析】试题分析:(1)利用直线与坐标轴的交点坐标,求出抛物线的解析式,利用翻折得出点C的坐标,就可求出直线BD的解析式;(2)本题利用路径最短的知识来解决问题;(3)由(1)的解析式设M(a,-a2+a+2),当△BOC∽△MON或△BOC∽△ONM时,由相似三角形的性质就可以求出结论.
试题解析:(1)易得A(-1,0),B(0,2),C(1,0).
设直线BD对应的函数解析式为y=kx+m.
把B(0,2),C(1,0)的坐标分别代入y=kx+m,
得![]() 解得
解得![]()
∴直线BD对应的函数解析式为y=-2x+2.
∵抛物线对应的函数解析式为y=-x2+bx+c.
∴把B(0,2),D(3,-4)的坐标分别代入y=-x2+bx+c,
得![]() 解得
解得![]()
∴抛物线对应的函数解析式为y=-x2+x+2.
(2)对称轴为:点A(-1,0)关于对称轴的对称点为E(2.0),连接BE交对称轴与点P,则BE的解析式为:y=-x+2 ,当x=![]() 时,BE与对称轴的交点坐标是P:(
时,BE与对称轴的交点坐标是P:(![]() ).
).
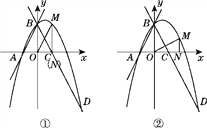
(3)存在,①如图①,当△MON∽△BCO时,![]() =
=![]() ,即
,即![]() =
=![]() ,∴MN=2ON.设ON=a,则M(a,2a),∴-a2+a+2=2a,解得a1=-2(不合题意,舍去),a2=1,∴M(1,2);②如图②,当△MON∽△CBO时,
,∴MN=2ON.设ON=a,则M(a,2a),∴-a2+a+2=2a,解得a1=-2(不合题意,舍去),a2=1,∴M(1,2);②如图②,当△MON∽△CBO时,![]() =
=![]() ,即
,即![]() =
=![]() ,∴MN=
,∴MN=![]() ON.设ON=n,则M
ON.设ON=n,则M![]() ,∴-n2+n+2=
,∴-n2+n+2=![]() ,解得n1=
,解得n1=![]() (不合题意,舍去),n2=
(不合题意,舍去),n2=![]() ,∴M(
,∴M(![]() ,
,![]() ).∴存在这样的点M(1,2)或
).∴存在这样的点M(1,2)或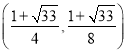 .
.


 互动英语系列答案
互动英语系列答案科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. “明天的降水概率是80%”表示明天会有80%的地方下雨
B. 为了解学生视力情况,抽取了500名学生进行调查,其中的样本是500名学生
C. 要了解我市旅游景点客流量的情况,采用普查的调查方式
D. 一组数据5,1,3,6,9的中位数是5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】袋中装有红色、黑色和绿色小球共360个,小明通过多次摸球试验后,得到红色、黑色和绿色小球的频率分别是25%、35%和40%,估计袋中有红球__________个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列运算正确的是( )
A.﹣2x2y3xy2=﹣6x2y2
B.(﹣x﹣2y)(x+2y)=x2﹣4y2
C.6x3y2÷2x2y=3xy
D.(4x3y2)2=16x9y4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系xOy中,△ABC的三个顶点坐标分别为A(-4,1)、B(-1,1)、C(-4,3).
(1)画出Rt△ABC关于原点O成中心对称的图形Rt△A1B1C1;
(2)若Rt△ABC与Rt△A2BC2关于点B中心对称,则点A2的坐标为 、C2的坐标为 .
(3)求点A绕点B旋转180°到点A2时,点A在运动过程中经过的路程.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里,装有三个分别标有数字1,2,3的小球,它们的形状、大小、质地等完全相同.小明先从盒子里随机取出一个小球,记下数字为x;放进盒子摇匀后,再由小华随机取出一个小球,记下数字为y.
(1)请用树状图或列表分析,写出(x,y)所有可能出现的结果;
(2)求小明、小华各取一次小球所确定的点(x,y)落在反比例函数![]() 图象上的概率.
图象上的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com