
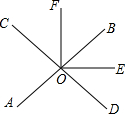
 如图,直线AB与CD相交于点O,OE平分∠BOD,OF⊥OE于点O,若∠AOC=60°,求∠BOF的度数.
如图,直线AB与CD相交于点O,OE平分∠BOD,OF⊥OE于点O,若∠AOC=60°,求∠BOF的度数.分析 直接利用角平分线的定义结合垂线的定义以及对顶角的性质分别分析得出答案.
解答 解:∵直线AB与CD相交于点O(已知),
∴∠BOD=∠AOC(对顶角相等),
∵∠AOC=60°( 已知),
∴∠BOD=60°(等量代换),
∵OE平分∠BOD( 已知 ),
∴∠BOE=$\frac{1}{2}$∠BOD=30°( 角平分线的性质)
∵OF⊥OE( 已知 ),
∴∠EOF=90°( 垂直定义 ),
∴∠BOF=∠EOF-∠BOE=60°.
故答案为:对顶角相等,60,BOD,角平分线的性质,垂直定义,60°.
点评 此题主要考查了角平分线的定义、垂线的定义以及对顶角的性质,正确把握相关性质是解题关键.


 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:填空题
 对于边长为4的等边△ABC,如图建立平面直角坐标系,则点A的坐标是(0,2$\sqrt{3}$),点B的坐标是(-2,0),点C的坐标是C(2,0).
对于边长为4的等边△ABC,如图建立平面直角坐标系,则点A的坐标是(0,2$\sqrt{3}$),点B的坐标是(-2,0),点C的坐标是C(2,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,线段AB=4,点O是线段AB上的点,点C、D是线段OA、OB的中点,小明很轻松地求得CD=2.他在反思过程中突发奇想:若点O在AB延长线上运动时,原有的结论“CD=2”是仍然成立呢?请帮小明画出图形分析并说明理由.
如图,线段AB=4,点O是线段AB上的点,点C、D是线段OA、OB的中点,小明很轻松地求得CD=2.他在反思过程中突发奇想:若点O在AB延长线上运动时,原有的结论“CD=2”是仍然成立呢?请帮小明画出图形分析并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
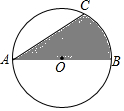 如图,AB是⊙O 的直径,C是⊙O 上一点,且AC=$\sqrt{3}$,∠CAB=30°.图中阴影部分的面积是$\frac{\sqrt{3}}{4}$+$\frac{π}{6}$.
如图,AB是⊙O 的直径,C是⊙O 上一点,且AC=$\sqrt{3}$,∠CAB=30°.图中阴影部分的面积是$\frac{\sqrt{3}}{4}$+$\frac{π}{6}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
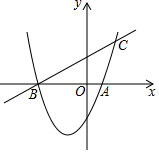 如图,已知抛物线y=ax2+bx-2(a≠0)与x轴交于A,B两点,直线BC交抛物线于点C,若点C的坐标为(2,3),tan∠CBA=$\frac{1}{2}$,求此抛物线的对称轴为直线x=-$\frac{3}{2}$.
如图,已知抛物线y=ax2+bx-2(a≠0)与x轴交于A,B两点,直线BC交抛物线于点C,若点C的坐标为(2,3),tan∠CBA=$\frac{1}{2}$,求此抛物线的对称轴为直线x=-$\frac{3}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com