
 ��ͼ����ABC�DZ߳�Ϊ4�ĵȱ������Σ�AD��BC��D��B��������ԭ���غϣ�C������Ϊ��4��0������P��Q�ֱ�ΪB��C����ͬʱ��������P��BC���յ�C�˶����ٶ�Ϊ1cm/s����Q��CA��AB���յ�B�˶����ٶ�Ϊ2cm/s���������˶���ʱ��Ϊt��s����
��ͼ����ABC�DZ߳�Ϊ4�ĵȱ������Σ�AD��BC��D��B��������ԭ���غϣ�C������Ϊ��4��0������P��Q�ֱ�ΪB��C����ͬʱ��������P��BC���յ�C�˶����ٶ�Ϊ1cm/s����Q��CA��AB���յ�B�˶����ٶ�Ϊ2cm/s���������˶���ʱ��Ϊt��s�������� ��1�����ݵȱ������ε����ʣ��ɵó�OD��AD�ij��ȣ��̶��ó���A�����ꣻ
��2����ͼ1���ɡ�ABCΪ�ȱ������εá�C=60�㣬���Ե���CPQ=30��ʱ��PQ��AC�����ݺ�30�ȵ�ֱ�����������ߵĹ�ϵ��CQ=$\frac{1}{2}$PC����2t=$\frac{1}{2}$��4-t����Ȼ��ⷽ�̼��ɣ�
��3������CQ=2t����C=60�㣬�ó�QE=CQ•sin60��=$\sqrt{3}$t���������������ɣ�Ȼ�����ö��κ��������ʼ��������PQD��������ֵ��
��4�����ݣ�1������õ�ֵ���ɷ�����������ۣ�
��� 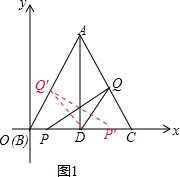 �⣺��1���ߡ�ABC�DZ߳�Ϊ4�ĵȱ������Σ�AD��BC��D��
�⣺��1���ߡ�ABC�DZ߳�Ϊ4�ĵȱ������Σ�AD��BC��D��
��OC=4��OD=CD=2��
��AD=$\sqrt{3}$OC=2$\sqrt{3}$��
���A��������2��2$\sqrt{3}$����
��2����ͼ1��BP=tcm��CQ=2tcm��
�ߡ�ABCΪ�ȱ������Σ�
���C=60�㣬
�൱��CPQ=30��ʱ��PQ��AC��
��CQ=$\frac{1}{2}$PC����2t=$\frac{1}{2}$��4-t�������t=$\frac{4}{5}$��
����t=$\frac{4}{5}$ʱ��PQ��AC��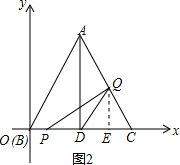
��3����ͼ2����QE��DC��E��
�ߵ�0��t��2ʱ��
CQ=2t����C=60�㣬
��QE=CQ•sin60��=$\sqrt{3}$t��
PD=2-t��
��S��PQD=$\frac{1}{2}$��PD��EQ=$\frac{1}{2}$��2-t��•$\sqrt{3}$t=-$\frac{\sqrt{3}}{2}$t2+$\sqrt{3}$t=-$\frac{\sqrt{3}}{2}$��t-1��2+$\frac{\sqrt{3}}{2}$����S=-$\frac{\sqrt{3}}{2}$��t-1��2+$\frac{\sqrt{3}}{2}$��0��t��2����
�൱t=1ʱ����PQD��������ֵΪ��$\frac{\sqrt{3}}{2}$��
��4����Ȼ��������x��ֵ��ʹ����PQΪֱ����Բ��AC���룬
��Q��AB��ʱ����ȻPQ����ֱ��AC��
�ɣ�1��֪����t=$\frac{4}{5}$��Q��AC�ϣ�ʱ��PQ��AC��
��ͼ1����P��Q���ABʱ��BP=t��BQ��=$\frac{1}{2}$��AC+AQ��=2t��
��AC=4��
��AQ��=2x-4��
��2t-4+$\frac{1}{2}$t=4��
��t=$\frac{16}{5}$��
��t=$\frac{16}{5}$ʱP��Q���AB��
������������t=$\frac{4}{5}$��PQ��AC��t=$\frac{16}{5}$ʱ��PQ��AB��
���Ե�x=$\frac{4}{5}$��$\frac{16}{5}$ʱ����PQΪֱ����Բ��AC���У�
��0��x��$\frac{4}{5}$��$\frac{4}{5}$��x��$\frac{16}{5}$��$\frac{16}{5}$��x��4ʱ����PQΪֱ����Բ��AC�ཻ��
���� �����ۺϿ����˵ȱ������ε����ʡ�ֱ�������ε����ʣ��������������Բ��ֱ�ߵ�λ�ù�ϵ������Ĺؼ����ö����ʱ��t���ٶȱ�ʾ�߶εij��ȣ�������һ�����ۺ��ԣ��Ѷ��еȣ�


 ������״Ԫ���Ծ�ϵ�д�
������״Ԫ���Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����O��ֱ��AB=2��P���ϰ�Բ��A��B���⣩����һ�㣬��APB��ƽ���߽���O��C����EF��AC��BC���е�M��N����EF�ij���$\sqrt{3}$��
��ͼ����O��ֱ��AB=2��P���ϰ�Բ��A��B���⣩����һ�㣬��APB��ƽ���߽���O��C����EF��AC��BC���е�M��N����EF�ij���$\sqrt{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ������ABCD�У�AB=a��BC=b������P��A���������A��B��C�ķ�����AB��BC���ƶ�����PA=x����D��ֱ��PA�ľ���Ϊy����y����x�ĺ���ͼ�������ͼ��
��ͼ������ABCD�У�AB=a��BC=b������P��A���������A��B��C�ķ�����AB��BC���ƶ�����PA=x����D��ֱ��PA�ľ���Ϊy����y����x�ĺ���ͼ�������ͼ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ABΪ��O��ֱ����AB=2BC=2��DE=DB����DB=$\frac{\sqrt{2}}{2}$��
��ͼ��ABΪ��O��ֱ����AB=2BC=2��DE=DB����DB=$\frac{\sqrt{2}}{2}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ�����κ�����ͼ����x�ύ��A��-3��0����B��1��0�����㣬��y���ڵ�C��0��3������C��D�Ƕ��κ���ͼ���ϵ�һ�ԶԳƵ㣮
��ͼ�����κ�����ͼ����x�ύ��A��-3��0����B��1��0�����㣬��y���ڵ�C��0��3������C��D�Ƕ��κ���ͼ���ϵ�һ�ԶԳƵ㣮�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com