
【题目】已知一条抛物线经过A(0,3),B(4,6)两点,对称轴是x=![]() .
.
(1)求这条抛物线的关系式.
(2)证明:这条抛物线与x轴的两个交点中,必存在点C,使得对x轴上任意点D都有AC+BC≤AD+BD.
【答案】(1)y=![]() .(2)证明见解析.
.(2)证明见解析.
【解析】本题主要考查了抛物线与x轴的交点和待定系数法求二次函数解析式
(1)先设出函数的解析式:y=ax2+bx+c,根据抛物线经过A(0,3),B(4,6)两点,用待定系数法求出函数的解析式;
(2)令y=0,得到方程,根据方程根与系数的关系求出抛物线与x轴的两个交点,再根据三角形任意两边之和大于第三边,来证明.
(1)解:设所求抛物线的关系式为y=ax2+bx+c,
∵A(0,3),B(4,6),对称轴是直线x=![]() .
.
∴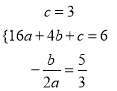 , 解得
, 解得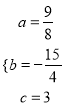
∴y=![]() .
.
(2)证明:令y=0,得![]() ="0," ∴
="0," ∴![]()
∵A(0,3),取A点关于x轴的对称点E,∴E (0,-3).
设直线BE的关系式为y=kx-3,把B(4,6)代入上式,得6=4k-3,
∴k=![]() ,∴y=
,∴y=![]() x-3 .
x-3 .
由![]() x-3=0,得x=
x-3=0,得x=![]() .
.
故C为![]() ,C点与抛物线在x轴上的一个交点重合,
,C点与抛物线在x轴上的一个交点重合,
在x轴上任取一点D,在△BED中,BE< BD+DE.
又∵BE=EC+BC,EC=AC,ED=AD,∴AC+BC<AD+BD.
若D与C重合,则AC+BC="AD+BD." ∴AC+BC≤AD+BD.


科目:初中数学 来源: 题型:
【题目】游泳池常需进行换水清洗,图中的折线表示的是游泳池换水清洗过程“排水—清洗—灌水”中水量y(m3)与时间t(min)之间的函数图象.
(1)根据图中提供的信息,求整个换水清洗过程水量y(m3)与时间t(min)的函数表达式;
(2)问排水、清洗、灌水各花多少时间?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级10个班师生举行毕业文艺汇演,每班2个节目,有歌唱与舞蹈两类节目,年级统计后发现歌唱类节目数比舞蹈类节目数的2倍少4个.
(1)九年级师生表演的歌唱与舞蹈类节目数各有多少个?
(2)该校七、八年级师生有小品节目参与,在歌唱、舞蹈、小品三类节目中,每个节目的演出平均用时分别是5分钟、6分钟、8分钟,预计所有演出节目交接用时共花15分钟.若从20:00开始,22:30之前演出结束,问参与的小品类节目最多能有多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明调查了全班本学期阅读课外书的情况,并根据统计数据,绘制如下的频率分布折线图和扇形统计图。
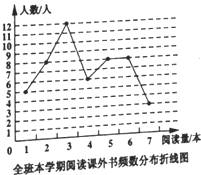
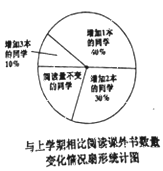
根据以上信息,回答下列问题:
①这个班共有__________ 名学生,本学期阅读量5本的有________ 人
②这个班本学期阅读量的中位数是_______ 本,众数是 ______ 本;
③求全班本学期比上学期每名同学的平均阅读量增加了多少本?
查看答案和解析>>
科目:初中数学 来源: 题型:
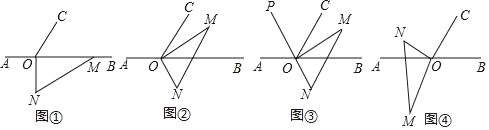
【题目】如图①,点O为直线AB上一点,过点O作射线OC,使∠AOC=120°,将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
(1)将图①中的三角板OMN摆放成如图②所示的位置,使一边OM在∠BOC的内部,当OM平分∠BOC时,∠BON= ;(直接写出结果)
(2)在(1)的条件下,作线段NO的延长线OP(如图③所示),试说明射线OP是∠AOC的平分线;
(3)将图①中的三角板OMN摆放成如图④所示的位置,请探究∠NOC与∠AOM之间的数量关系.(直接写出结果,不须说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程组解应用题:某学校在筹建数学实验室过程中,准备购进一批桌椅,现有三种桌椅可供选择:甲种每套150元,乙种每套210元,丙种每套250元。若该学校同时购买其中两种不同型号的桌椅50套,恰好花费了9000元,则共有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,矩形ABCD的边AB=3,AD=2,将此矩形置入直角坐标系中,使AB在x 轴上,点C 在直线y=x-2上.
(1)求矩形各顶点坐标;
(2)若直线y=x-2与y轴交于点E,抛物线过E、A、B三点,求抛物线的关系式;
(3)判断上述抛物线的顶点是否落在矩形ABCD内部,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
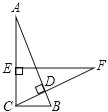
【题目】如图,Rt△ABC中,∠ACB=90°, BC=3cm, CD⊥AB于D, 在AC上取一点E,使EC=BC,过点E作EF⊥AC交CD的延长线于点F,若EF=5cm,求AE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com