

���� ��1��ֱ�����õ���ֱ�������ε����ʽ������̼��ɣ�
��2�������CP=$\frac{4}{3}$CE�������ó�CP=9-3t�������������⼴�ɣ�
��3�����������������ֱ���������У�����������Ǻ�������������⼴�ɣ�
��4����5��������������ε������ʽ������������ʱ��ĺ�����ϵʽ�����Ƚϼ��ɵó����ۣ�
��� �⣺��1�����˶�֪��CE=$\frac{4}{3}$t��AP=3t��
��AC=9��
��PC=9-3t��
�ߡ�PCE�ǵ���ֱ�������Σ�
��PC=EC��
��9-3t=$\frac{4}{3}$t��
��t=$\frac{27}{13}$��
�ʴ�Ϊ��$\frac{27}{13}$��
��2����ͼ1��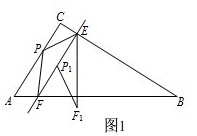 �����⣬��PEF=��P1EF1��
�����⣬��PEF=��P1EF1��
��EF��AC����C=90�㣬
���BEF=90�㣬
��CPE=��PEF��
��EF1��AB��
���B=��P1EF1��
���CPE=��B��
��tan��CPE=tanB=$\frac{AC}{BC}$=$\frac{3}{4}$��
��tan��CPE=$\frac{CE}{CP}$��
��$\frac{CE}{CP}$=$\frac{3}{4}$��
��CP=$\frac{4}{3}$CE��
��AP=3t��0��t��3����CE=$\frac{4}{3}$t��
��CP=9-3t��
��9-3t=$\frac{4}{3}$��$\frac{4}{3}$t�����t=$\frac{81}{43}$��
��3����ͼ2��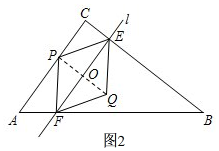 ����PQ��EF�ڵ�O��
����PQ��EF�ڵ�O��
��P��Q����ֱ��EF�Գƣ�
��EF��ֱƽ��PQ��
���ı���PEQFΪ���Σ���OE=OF=$\frac{1}{2}$ EF
�ٵ���P��AC�����˶�ʱ��
��֪�ı���POECΪ���Σ�
��OE=PC��
��PC=$\frac{1}{2}$EF��
��CE=$\frac{4}{3}$t��
��BE=12-$\frac{4}{3}$t��EF=BE•tanB=$\frac{3}{4}$��12-$\frac{4}{3}$t��=9-t��
��9-3t=$\frac{1}{2}$��9-t�������t=$\frac{9}{5}$��
�ڵ���P��CB�����˶�ʱ��P��E��Q���㹲�ߣ��������ı���PEQF��
����ͼ3��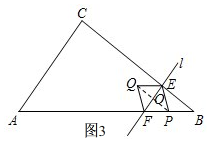 ����P��BA�����˶�ʱ�����P�ڵ�B��F֮�䣬
����P��BA�����˶�ʱ�����P�ڵ�B��F֮�䣬
��BE=12-$\frac{4}{3}$t��
��BF=$\frac{BE}{cosB}$=$\frac{5}{4}$��12-$\frac{4}{3}$t��=15-$\frac{5}{3}$t��
��BP=5��t-6����
��PF=BF-BP=15-$\frac{5}{3}$t-5��t-6��=45-$\frac{20}{3}$t��
�ߡ�POF=��BEF=90�㣬
��PO��BE��
���OPF=��B��
��Rt��POF��sin��OPF=sinB��
��$\frac{OF}{PE}$=$\frac{3}{5}$��
��$\frac{\frac{1}{2}��9-t��}{45-\frac{20}{3}t}=\frac{3}{5}$�����t=$\frac{45}{7}$��
�൱t=$\frac{9}{5}$��t=$\frac{45}{7}$ʱ���ı���PEQFΪ���Σ�
��4����Rt��ABC�У����ݹ��ɶ������ã�BC=12��
����P�ڱ�AC��ʱ��0��t��3��
����P�ڱ�BC��ʱ��
��P�͵�E�غ�ʱ��4��t-3��=$\frac{4}{3}$t��
��t=4.5��
��P�պõ���Bʱ��t=6��
����P�ڱ�AB��ʱ���Һ͵�F�غ�ʱ��
��l��AC��
���BEF�ס�BCA��
��$\frac{BE}{BC}=\frac{BF}{AB}$��
��$\frac{CE}{BC}=\frac{AF}{AB}$��
��$\frac{\frac{4}{3}t}{12}=\frac{15-5��t-6��}{15}$��
��t=6.75��
�ٵ�0��t��6ʱ����ͼ4��
���˶�֪��CE=$\frac{4}{3}$t��
��BE=12-$\frac{4}{3}$t��
��EF��AC��
���BEF�ס�BCA��
��$\frac{BE}{BC}=\frac{EF}{AC}$��
��$\frac{12-\frac{4}{3}t}{12}=\frac{EF}{9}$��
��EF=9-t��
��S��PEF=$\frac{1}{2}$EF•CE=$\frac{1}{2}$��9-t����$\frac{4}{3}$t=-$\frac{2}{3}$��t-$\frac{9}{2}$��2+$\frac{27}{2}$��
��ʱ��t=3ʱ��S��PEF���=-$\frac{2}{3}$��3-$\frac{9}{2}$��2+$\frac{27}{2}$=12��
�ڵ�3��t��4.5ʱ����ͼ5��
���˶�֪��PE=$\frac{4}{3}$t-4��t-3��=-$\frac{8}{3}$t+12��
��S��PEF=$\frac{1}{2}$EF•PE=$\frac{1}{2}$��9-t����-$\frac{8}{3}$t+12��=$\frac{4}{3}$t2-18t+54��
��ʱ���������ֵ��
�۵�4.5��t��6ʱ����ͼ6��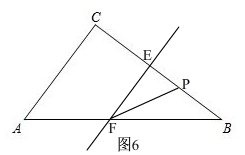
ͬ�ڵķ������ã�S��PEF=-$\frac{4}{3}$t2+18t-54=-$\frac{4}{3}$��t-$\frac{27}{4}$��2+$\frac{27}{4}$
��ʱ����t=6ʱ��S��PEF���=6��
�ܵ�6��t��6.75ʱ����ͼ7��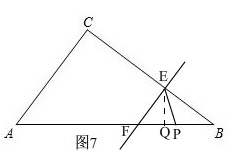
��Rt��ABC��sin��B=$\frac{AC}{AB}$=$\frac{9}{15}$=$\frac{3}{5}$��
��Rt��BEQ��sin��B=$\frac{QE}{BE}$=$\frac{QE}{12-\frac{4}{3}t}$=$\frac{3}{5}$��
��QE=$\frac{1}{5}$��36-4t������Rt��BEF��sin��B=$\frac{EF}{BF}$=$\frac{9-t}{BF}$=$\frac{3}{5}$��
��BF=$\frac{5}{3}$��9-t����
��PF=BF-BP=$\frac{5}{3}$��9-t��-5��t-6��=45-$\frac{20}{3}$t
S��PEF=$\frac{1}{2}$PF•QE=$\frac{8}{3}$t2-42t+162��
��ʱ���������ֵ��
�ݵ�6.75��t��9ʱ����ͼ8��
ͬ�ܵķ������ã�S��PEF=-$\frac{8}{3}$t2+42t-162��
���ڶԳ���t=$\frac{63}{4}$��9��
���ʱȡ�������ֵ��
���������˶������У�S�����ֵΪ12��
���� �������ı����ۺ��⣬��Ҫ������ֱ�������ε����ʣ�����ֱ�������ε����ʣ����������ε����ʺ��ж��������ε������ʽ����ת�����ʣ��⣨1���Ĺؼ��ǵó�CP=CE���⣨2���Ĺؼ�����CP=$\frac{4}{3}$CE����������⣬�⣨3����4���Ĺؼ��ǻ���ͼ�Σ���һ���ѶȱȽϴ�����Ҳ�Ƚϴ���п�ѹ���⣮


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
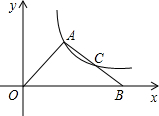 ��ͼ����AOB�У���CΪ��AB���е㣬����������y=$\frac{k}{x}$��k��0����ͼ��A��C���㣬����AOB�����Ϊ12����k��ֵ�ǣ�������
��ͼ����AOB�У���CΪ��AB���е㣬����������y=$\frac{k}{x}$��k��0����ͼ��A��C���㣬����AOB�����Ϊ12����k��ֵ�ǣ�������| A�� | 8 | B�� | 7.5 | C�� | 6 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪A��B�������100km�����������ﳵͬʱ�ֱ��A��B����������У��������Ƕ�����������ʻ������������A�صľ���s��ǧ�ף����ﳵʱ��t��Сʱ������ĺ�����ϵͼ����ͼ��ʾ����������������ʱ���Ҿ���A��$\frac{300}{7}$km��
��֪A��B�������100km�����������ﳵͬʱ�ֱ��A��B����������У��������Ƕ�����������ʻ������������A�صľ���s��ǧ�ף����ﳵʱ��t��Сʱ������ĺ�����ϵͼ����ͼ��ʾ����������������ʱ���Ҿ���A��$\frac{300}{7}$km���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
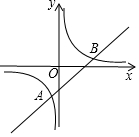 ��ͼ����ƽ��ֱ������ϵxOy�У�ֱ��y=kx-3��˫����y=$\frac{4}{x}$����������ΪA��B������A��-1��m����
��ͼ����ƽ��ֱ������ϵxOy�У�ֱ��y=kx-3��˫����y=$\frac{4}{x}$����������ΪA��B������A��-1��m�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3 | B�� | 4 | C�� | 5 | D�� | 6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| �༶ | �μ����� | ��λ�� | ���� | ƽ���� |
| ��1���� | 50 | 120 | 103 | 122 |
| ��2���� | 49 | 121 | 201 | 122 |
| A�� | ����ƽ���ɼ�һ�� | B�� | ��1����������������ڣ�2���� | ||
| C�� | ��2����������ֻ��ȣ�1�������� | D�� | ��1���������ɼ��ȶ�һЩ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com