
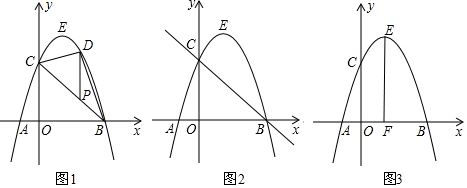
���� ��1�����ô���ϵ��������A��B����������������ߵĽ���ʽ��ת��Ϊ�ⷽ���鼴�ɣ�
��2����P��a��3-a������D��a��-a2+2a+3��������S��BDC=S��PDC+S��PDB���������κ��������ö��κ��������ʽ�����ɣ�
��3�����ȹ�C��CH��EF��H�㣬��CH=EH=1��Ȼ��ֱ�ӵ�M��EF�����M��EF�Ҳ�ʱȥ������⼴����ô𰸣�
��� �⣺��1����������y=-x2+bx+c��ͼ����A��-1��0����B��3��0����
��$\left\{\begin{array}{l}{-1-b+c=0}\\{-9+3b+c=0}\end{array}\right.$�����$\left\{\begin{array}{l}{b=2}\\{c=3}\end{array}\right.$��
�������߽���ʽΪy=-x2+2x+3��
��������E��1��4����
��2����ͼ1�У�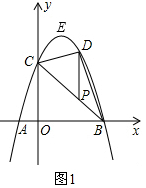
��B��3��0����C��0��3��
��ֱ��BC�Ľ���ʽΪy=-x+3��
��P��a��3-a������D��a��-a2+2a+3����
��PD=��-a2+2a+3��-��3-a��=-a2+3a��
��S��BDC=S��PDC+S��PDB=$\frac{1}{2}$PD•a+$\frac{1}{2}$PD•��3-a��=$\frac{1}{2}$PD•3��
=$\frac{3}{2}$��-a2+3a��=-$\frac{3}{2}$��a-$\frac{3}{2}$��2+$\frac{27}{8}$��
��-$\frac{3}{2}$��0��
�൱a=$\frac{3}{2}$ʱ����BDC��������ʱP��$\frac{3}{2}$��$\frac{3}{2}$����
��3����ͼ2�У�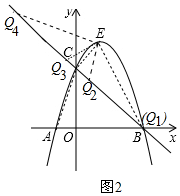
��C��0��3����E��1��4����B��3��0����
��ֱ��EC�Ľ���ʽΪy=x+3��ֱ��BC�Ľ���ʽΪy=-x+3��
��1����-1��=-1��
��EC��BC��
���ECB=90�㣬
�൱$\frac{EC}{CO}$=$\frac{CQ}{OA}$��$\frac{EC}{OA}$=$\frac{CQ}{CO}$ʱ����Q��C��E�����ɵ����������AOC���ƣ�
��$\frac{\sqrt{2}}{3}$=$\frac{CQ}{1}$��$\frac{\sqrt{2}}{1}$=$\frac{CQ}{3}$��
��CQ=$\frac{\sqrt{2}}{3}$��3$\sqrt{2}$��
��Q1��3��0����Q2��$\frac{1}{3}$��$\frac{8}{3}$����
���ݶԳ��Կ�֪��Q3��-$\frac{1}{3}$��$\frac{10}{3}$����Q4��-3��6��ʱҲ����������
����������Q��������3��0������-3��6������$\frac{1}{3}$��$\frac{8}{3}$������-$\frac{1}{3}$��$\frac{10}{3}$����
��4����ͼ3�У���C��CH��EF��H�㣬��CH=EH=1��
��M��EF���ʱ��
�ߡ�MNC=90�㣬
���MNF�ס�NCH��
��$\frac{MF}{NH}$=$\frac{FN}{BC}$��
��FN=n����NH=3-n��
��$\frac{1-m}{3-n}$=$\frac{n}{1}$��
��n2-3n-m+1=0��
����n�ķ����н⣬��=��-3��2-4��-m+1����0��
��m��-$\frac{5}{4}$��
��M��EF�Ҳ�ʱ��Rt��CHE�У�CH=EH=1����CEH=45�㣬����CEF=45�㣬
��EM��CE��x���ڵ�M�����FEM=45�㣬
��FM=EF=4��
��OM=5��
��NΪ��Eʱ��OM=5����ʱm��ֵ���
��m��5��
��m�����ֵΪ5����СֵΪ-$\frac{5}{4}$��
�ʴ�Ϊ5��-$\frac{5}{4}$��
���� ���⿼����κ����ۺ��⡢һ�κ��������������ε��ж������ʡ���Ԫһ�η��̵��б�ʽ��֪ʶ������Ĺؼ������������ѧ֪ʶ������⣬ѧ�ṹ�����κ��������ֵ���⣬ѧ���÷������۵�˼��˼�����⣬ѧ����ת����˼��˼�����⣬�����п�ѹ���⣮


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
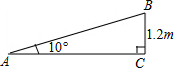 һ����������ǰ��̨�߳�����1.2�ף�̨�ײ�����ɹ��������ߵ�б�£�������ͼ��ʾ�������й�ϵ����۴�����ǣ�������
һ����������ǰ��̨�߳�����1.2�ף�̨�ײ�����ɹ��������ߵ�б�£�������ͼ��ʾ�������й�ϵ����۴�����ǣ�������| A�� | б��AB���½���10�� | B�� | б��AB���¶���tan10�� | ||
| C�� | AC=1.2tan10���� | D�� | AB=$\frac{1.2}{sin10��}$�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x2-4x+3=0 | B�� | x2+3x+4=0 | C�� | x2+4x-3=0 | D�� | x2+3x-4=0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ���ӻ��������ڲ��Ź�� | B�� | ����������ˣ���������� | ||
| C�� | ��������� | D�� | ��һöӲ�ң����泯�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2xy+x2=1 | B�� | y2=ax+2 | C�� | y=x2-2 | D�� | x2-y2+4=0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
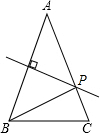 ��ͼ����ABC�У�AB=AC��AB�Ĵ�ֱƽ���߽�AC��P�㣮
��ͼ����ABC�У�AB=AC��AB�Ĵ�ֱƽ���߽�AC��P�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ������ѧʵ�����У�С��Ϊ�˲���ѧУ���CD�ĸ߶ȣ��ڵ���A�����ø߶�Ϊ1.5�IJ����AB�������˶���D������Ϊ32�㣬ACΪ22�ף������CD�ĸ߶�ԼΪ15.1�ף��������ȷ��0.1�ף��ο����ݣ�sin32��=0.53��cos32��=0.85��tan32��=0.62��
��ͼ������ѧʵ�����У�С��Ϊ�˲���ѧУ���CD�ĸ߶ȣ��ڵ���A�����ø߶�Ϊ1.5�IJ����AB�������˶���D������Ϊ32�㣬ACΪ22�ף������CD�ĸ߶�ԼΪ15.1�ף��������ȷ��0.1�ף��ο����ݣ�sin32��=0.53��cos32��=0.85��tan32��=0.62���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����Rt��ABC�У���ACB=90�㣬AC=6��BC=8��
��ͼ����Rt��ABC�У���ACB=90�㣬AC=6��BC=8���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com