分析:①观察直线y=k
1x+b和反比例函数
y=的图象的交点坐标,即可判定方程组
的解是否正确;
②观察直线y=k
1x+b位于反比例函数
y=的图象上方的部分对应的x的取值,即可判断是否正确.
③利用待定系数法分别求出直线y=k
1x+b和反比例函数
y=的解析式,从而可知k
2、b、k
1与0的关系;
④根据直线y=k
1x+b的解析式,首先求出它与两坐标轴的交点,然后由三角形的面积公式可求出结果.
解答:解:①观察图象,发现直线y=k
1x+b和反比例函数y′=
的图象交于点(-2,1),(1,-2),
则方程组
的解为
,
.正确;
②观察图象,可知当-6<x<0或0<x<1时,有y>y′.错误;
③∵反比例函数y′=
,的图象经过点(-2,1),
∴k
2=-2×1=-2,
∴y=-
.
∵直线y=k
1x+b经过点(-2,1)和点(1,-2),
∴
,
∴
,
∴y=-x-1.
∴k
1<0,k
2<0,b<0,正确;
④∵y=-x-1,
∴当y=0,x=-1.∴此直线与x轴交点的坐标是(-1,0),
当x=0时,y=-1.∴此直线与y轴交点的坐标是(0,-1).
∴△ABO的面积是
×1×1=
,正确.
故选B.
点评:本题考查了用待定系数法求函数的解析式,求三角形的面积,函数图象与方程组的解的关系,体现了数形结合的思想.

 如图,下列结论中错误的是( )
如图,下列结论中错误的是( )

 精英口算卡系列答案
精英口算卡系列答案
 的解为
的解为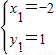
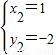


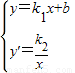 的解为
的解为
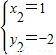


 的解为
的解为

