
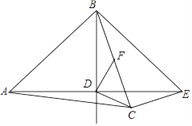
【题目】如图,在△ABC中,AB=AC,点D是△ABC内一点,AD=BD,且AD⊥BD,连接CD.过点C作CE⊥BC交AD的延长线于点 E,连接BE.过点D作DF⊥CD交BC于点F.
(1)若BD=DE=![]() ,CE=
,CE=![]() ,求BC的长;
,求BC的长;
(2)若BD=DE,求证:BF=CF.
【答案】(1)BC=2![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】试题分析:(1)利用勾股定理求出BE的长,进而再次利用勾股定理求出BC的长;
(2)连接AF,首先利用ASA证明出△BDF≌△EDC,得到![]() ,进而得到∠ADF=∠BDC,再次利用SAS证出△ADF≌△BDC,结合题干条件得到AF⊥BC,利用等腰三角形的性质得到结论.
,进而得到∠ADF=∠BDC,再次利用SAS证出△ADF≌△BDC,结合题干条件得到AF⊥BC,利用等腰三角形的性质得到结论.
试题解析:(1)∵BD⊥AD,点E在AD的延长线上,
∴![]()
∵![]()
∴![]()
∵BC⊥CE,
∴![]()
∴![]()
(2)连接AF,

∵CD⊥BD,DF⊥CD,
∴![]()
∴∠BDF=∠CDE,
∵CE⊥BC,
∴![]()
∴∠DBC=∠CED,
在△BDF和△EDC中,
∵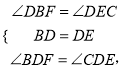
∴△BDF≌△EDC(ASA),
∴DF=CD,
∴![]()
∵∠ADB=∠CDF,
∴∠ADB+∠BDF=∠CDF+∠BDF,
∴∠ADF=∠BDC,
在△ADF和△BDC中,
∵
∴△ADF≌△BDC(SAS),
∴∠AFD=∠BCD,
∴![]()
∴![]()
∴AF⊥BC,
∴AB=AC,
∴BF=CF.


 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案科目:初中数学 来源: 题型:
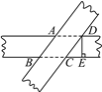
【题目】如图所示,将两条宽度相同的纸条交叉重叠放在一起,则重叠部分ABCD是________形,若纸条宽DE=4 cm,CE=3 cm,则四边形ABCD的面积为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线l : ![]() 经过定点P,交x、y轴于A、B两点.
经过定点P,交x、y轴于A、B两点.
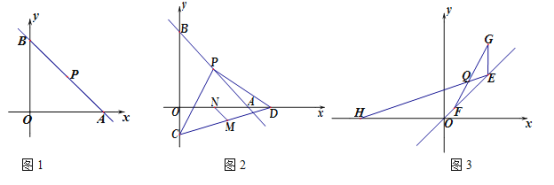
(1)如图1,直接写出点P的坐标__________________;
(2)如图2,当k=—1时,点C为y轴负半轴上一动点,过点P作PD⊥PC交x轴于点D,M、N分别为CD、OA的中点,求![]() 的值;
的值;
(3)如图3,E、F两点在射线OP上移动,EF=![]() ,点E向上移动2个单位得到点G,点E横坐标为 t(t>0),在x轴负半轴上有点H(—2t,0),FG与HE相交于Q点,求证:点Q在某条直线上运动,并求此直线的解析式.
,点E向上移动2个单位得到点G,点E横坐标为 t(t>0),在x轴负半轴上有点H(—2t,0),FG与HE相交于Q点,求证:点Q在某条直线上运动,并求此直线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知平面上点![]() ,
,![]() ,
,![]() ,
,![]() (每三点都不在一条直线上).
(每三点都不在一条直线上).
(1)经过这四点最多能确定 条直线.
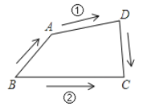
(2)如图这四点表示公园四个地方,如果点![]() ,
,![]() 在公园里湖对岸两处,
在公园里湖对岸两处,![]() ,
,![]() 在湖面上,要从
在湖面上,要从![]() 到
到![]() 筑桥,从节省材料的角度考虑,应选择图中两条路中的哪一条?如果有人想在桥上较长时间观赏湖面风光,应选择哪一条?为什么?
筑桥,从节省材料的角度考虑,应选择图中两条路中的哪一条?如果有人想在桥上较长时间观赏湖面风光,应选择哪一条?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两张等宽的纸条交叉重叠在一起,重叠的部分为四边形ABCD,若测得A,C之间的距离为12cm,点B,D之间的距离为16m,则线段AB的长为![]()
![]()
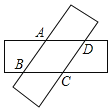
A. ![]() B. 10cmC. 20cmD. 12cm
B. 10cmC. 20cmD. 12cm
查看答案和解析>>
科目:初中数学 来源: 题型:
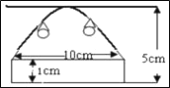
【题目】如图,是某河上一座古拱桥的截面图,拱桥桥洞上沿是抛物线形状,抛物线两端点与水面的和距离都是1m,拱桥的跨度为10m,桥洞与水面的最大距离是5m,桥洞两侧壁上各有一盏距离水面4m的景观灯,建立适当坐标系.
(1)求抛物线的解析式.
(2)求两盏景观灯之间的水平距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将若干个奇数按每行8个数排成如图的形式:

小军画了一方框框住了其中的9个数.
(1)如图中方框内9个数之和是 ;
(2)若小军画的方框内9个数之和等于333,则这个方框内左下角的那个数为_________;
(3)试说明:方框内的9个数之和总是9的倍数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上A、B两点分别对应有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a﹣b|,利用数形结合思想回答下列问题:
(1)数轴上表示2和10两点之间的距离是_______.
(2)数轴上一个点到表示2的点的距离为5.2,这个点表示的数为______.
(3)若x表示一个数,数轴上表示x和﹣5的两点之间的距离是____;(用含x的式子表示)
(4)若x表示一个数,|x+1|+|x﹣2|的最小值是______,相应的x的取值范围_______.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,同心圆中,大圆O的弦AB与小圆O切于点P,且AB=16,则圆环面积为________;
(2)如图2,同心圆中,大圆O的弦AB与小圆O相交,其中一个交点为点P,且AP=2,PB=8,则圆环面积为________.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com