
 =tan∠BAD=tan60°,AD=
=tan∠BAD=tan60°,AD=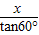 ,
,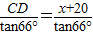 ,
, ,
,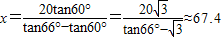 ,
,

科目:初中数学 来源: 题型:
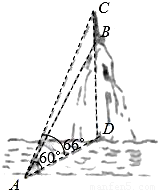
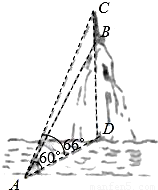
 某数学兴趣小组在学习了《锐角三角函数》以后,开展测量物体高度的实践活动,他们在河边的一点A测得河对岸小山顶上一座铁塔的塔顶C的仰角为66°、塔底B的仰角为60°,已知铁塔的高度BC为20m(如图),你能根据以上数据求出小山的高BD吗?若不能,请说明理由;若能,请求出小山的高BD.(精确到0.1m)(参考数据:sin66°≈0.9135,cos66°≈0.4067,tan66°≈2.2460)
某数学兴趣小组在学习了《锐角三角函数》以后,开展测量物体高度的实践活动,他们在河边的一点A测得河对岸小山顶上一座铁塔的塔顶C的仰角为66°、塔底B的仰角为60°,已知铁塔的高度BC为20m(如图),你能根据以上数据求出小山的高BD吗?若不能,请说明理由;若能,请求出小山的高BD.(精确到0.1m)(参考数据:sin66°≈0.9135,cos66°≈0.4067,tan66°≈2.2460)查看答案和解析>>
科目:初中数学 来源:第21章《解直角三角形》中考题集(35):21.5 应用举例(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:第4章《锐角三角形》中考题集(34):4.3 解直角三角形及其应用(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2007年全国中考数学试题汇编《锐角三角函数》(07)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com