
 ��ͼ����ƽ��ֱ������ϵ��A��-2��0����B��0��1����AB=AC���ҡ�BAC=90�㣮
��ͼ����ƽ��ֱ������ϵ��A��-2��0����B��0��1����AB=AC���ҡ�BAC=90�㣮���� ��1����CN��x���ڵ�N��ͨ���ǵļ���ó���NAC=��OBA�������ȵ�ֱ���Լ�AC=AB����֤��Rt��CNA��Rt��AOB��AAS���������ó�ON��CN�ij��ȣ�����ý⣻
��2���跴������������ʽΪy=$\frac{k}{x}$��C�䣨c��2��������ƽ�Ƶ����ʽ�ϵ�B��C�����꼴�ɵó���B������꣬�ٸ��ݷ���������ͼ���ϵ�������������ɵó�����k��c�Ķ�Ԫһ�η����飬�ⷽ���鼴�ɵó�k��cֵ���ɴ˼��ɵó���������������ʽ���B�䡢C�����꣬���ݵ�B�䡢C���������ô���ϵ�����������ֱ��B��C��Ľ���ʽ��
��3��������ڣ�����ֱ��B��C��Ľ���ʽ���������G�����꣬���M��t��0��������ƽ���ı��ε����ʼ��ɵó���P�����꣬�����÷���������ͼ���ϵ�������������ɵó�����t�ķ�ʽ���̣��ⷽ�̼��ɵó�tֵ����tֵ�����M��P�����꼴�ɵó����ۣ�
��� �⣺��1����CN��x���ڵ�N����ͼ1��ʾ��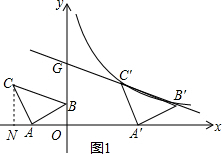
�ߡ�BAC=90�㣬
���NAC+��OAB=90�㣬
�ߡ�OAB+��OBA=90�㣬
���NAC=��OBA��
��Rt��CNA��Rt��AOB��$\left\{\begin{array}{l}{��CNA=��AOB}\\{��NAC=��OBA}\\{AC=AB}\end{array}\right.$��
��Rt��CNA��Rt��AOB��AAS����
��AN=BO=1��NO=NA+AO=3��CN=AO=2��
��C��������-3��2����
��2���跴������������ʽΪy=$\frac{k}{x}$��
��C��-3��2����B��0��1����
����C�䣨c��2������B�䣨c+3��1����
�ߵ�B���C���ڷ���������ͼ���ϣ�
��$\left\{\begin{array}{l}{k=2c}\\{k=c+3}\end{array}\right.$����ã�$\left\{\begin{array}{l}{c=3}\\{k=6}\end{array}\right.$��
�෴������������ʽΪy=$\frac{6}{x}$��
��c=3��
��C�䣨3��2����B�䣨6��1����
��ֱ��B��C��Ľ���ʽΪy=mx+n��
��$\left\{\begin{array}{l}{2=3m+n}\\{1=6m+n}\end{array}\right.$����ã�$\left\{\begin{array}{l}{m=-\frac{1}{3}}\\{n=3}\end{array}\right.$��
��ֱ��B��C��Ľ���ʽλy=-$\frac{1}{3}$x+3��
��3��������ڣ�
��y=-$\frac{1}{3}$x+3��x=0����y=3��
��G��0��3����
���M��t��0������P��0+3-t��3+2-0��������3-t��5����
�ߵ�P�ڷ���������y=$\frac{6}{x}$��ͼ���ϣ�
��5=$\frac{6}{3-t}$����ã�t=$\frac{9}{5}$��
������t=$\frac{9}{5}$�Ƿ���5=$\frac{6}{3-t}$�Ľ⣬
��M��$\frac{9}{5}$��0����P��$\frac{6}{5}$��5����
�ʴ���x���ϵĵ�M�ͷ���������ͼ���ϵĵ�P��ʹ���ı���PGMC����ƽ���ı��Σ���M������Ϊ��$\frac{9}{5}$��0������P������Ϊ��$\frac{6}{5}$��5����
���� ���⿼���˷���������ͼ���ϵ������������ȫ�������ε��ж��������Լ����ʽ���̣�����Ĺؼ��ǣ���1�����ON��CN�ij��ȣ���2�����÷���������ͼ���ϵ����������ҳ�����k��c�Ķ�Ԫһ�η����飻��3�����÷���������ͼ���ϵ�����������ҳ�����t�ķ�ʽ���̣����������е��⣬�ѶȲ������������Ŀʱ�����ݷ���������ͼ���ϵ�����������ҳ����̣����飩�ǹؼ���


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ֱ��l1�Ľ���ʽΪy=3x-3����l1��x �ύ�ڵ�D��ֱ��l2������A��B��ֱ��l1��l2���ڵ�C��
��ͼ��ֱ��l1�Ľ���ʽΪy=3x-3����l1��x �ύ�ڵ�D��ֱ��l2������A��B��ֱ��l1��l2���ڵ�C���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com