
 ��ͼ����ƽ��ֱ������ϵxOy�У���֪��P��-1��0����C��$\sqrt{2}$-1��1����D��0��-3����A��B��x���ϣ���PΪAB�е㣬S��CAP=1��
��ͼ����ƽ��ֱ������ϵxOy�У���֪��P��-1��0����C��$\sqrt{2}$-1��1����D��0��-3����A��B��x���ϣ���PΪAB�е㣬S��CAP=1������ ��1���ȸ��������������ʽ���AP=2��������PΪAB�е��ȷ��A���B��֮�䣬Ȼ�����ý���ʽ�������߽���ʽ��
��2����ͼ1�����÷��۵����ʵõ�ͼ��G�Ľ���ʽΪy=x2+2x-3��x��-3��x��1����y=-x2-2x+3��-3��x��1���������������ε�Q��������Ϊ1��Ȼ��ⷽ��x2+2x-3=1��-x2-2x+3=1�ɵõ���Q�����ꣻ
��3����ͼ2�������������N����x��ԳƵ�N�䣨0��1������D���ڶԳ���ĶԳƵ�D�䣨-2��-3��������N��D�佻x����E����ֱ��x=-1�ڵ�F������������֮���߶���̿��жϴ�ʱ��M�˶�����·����̣������ô���ϵ�������ֱ��N��D��Ľ���ʽ��Ȼ��ȷ��E���F������꣮
��� �⣺��1����S��CAP=1��C��$\sqrt{2}$-1��1����
��$\frac{1}{2}$•AP•1=1��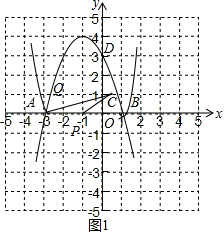
��AP=2��
��PΪAB�е㣬P��-1��0����
��A��-3��0����B��1��0����
���A��B��D����������ߵı���ʽΪy=a��x+3����x-1����
��D��0��3�������a•3•��-1��=3�����a=1��
���A��B��D����������ߵı���ʽΪy=x2+2x-3��
��2����ͼ1��������y=x2+2x-3��x�ᷭ�����õ��������߹�ϵʽΪy=-x2-2x+3��
��ͼ��G�Ľ���ʽΪy=x2+2x-3��x��-3��x��1����y=-x2-2x+3��-3��x��1��
��S��APQ=S��APC=1��
���Q��x��ľ���Ϊ1��
���Q��������Ϊ1��
��x2+2x-3=1��-x2-2x+3=1��
���x2+2x+3=1��x1=-1+$\sqrt{5}$��x2=-1-$\sqrt{5}$���ⷽ��-x2-2x+3=1��x1=-1+$\sqrt{3}$��x2=-1-$\sqrt{3}$��
������Q�����������-1+$\sqrt{5}$��1������-1-$\sqrt{5}$��1������-1+$\sqrt{3}$��1������-1-$\sqrt{3}$��1����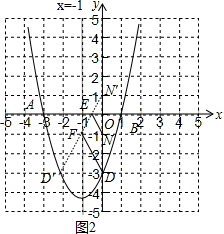
��3����ͼ2��
��N��0��-1����
���N����x��ԳƵ�N�䣨0��1����
�ߵ�D��0��-3����
���D���ڶԳ���ĶԳƵ�D�䣨-2��-3����
����N��D�佻x����E����ֱ��x=-1�ڵ�F��
��EN=EN�䣬FD=FD�䣬
��NE+EF+FD=EN��+EF+FD��=N��D�䣬
���ʱ��M�˶�����·����̣�
��ֱ��N��D��Ľ���ʽΪy=kx+b��
��N�䣨0��1����D�䣨-2��-3�������$\left\{\begin{array}{l}{b=1}\\{-2k+b=-3}\end{array}\right.$�����$\left\{\begin{array}{l}{k=2}\\{b=1}\end{array}\right.$��
��ֱ��N��D��Ĺ�ϵʽΪy=2x+1��
��E��-$\frac{1}{2}$��0����
��x=-1ʱ��y=-1��
��F��-1��-1����
���� ���⿼������������x��Ľ��㣺������κ���y=ax2+bx+c��a��b��c�dz�����a��0����x��Ľ�����������ת��Ϊ�����x��һԪ���η��̣���������֮���߶���̽����3���ʵ����·�����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | 3 | C�� | 4 | D�� | 5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0 | B�� | 1 | C�� | 2 | D�� | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
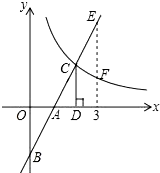 ��ͼ����ֱ������ϵ�У�ֱ��y1=2x-2�������ύ��A��B���㣬��˫����y2=$\frac{k}{x}$��x��0�����ڵ�C������C��CD��x�ᣬ����ΪD����OA=AD�������½��ۣ�
��ͼ����ֱ������ϵ�У�ֱ��y1=2x-2�������ύ��A��B���㣬��˫����y2=$\frac{k}{x}$��x��0�����ڵ�C������C��CD��x�ᣬ����ΪD����OA=AD�������½��ۣ��鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com