

���� ��1������ת�����ʵó�A��C=AC����A��=��BAC=60�㣬�������ε����ʵó���ACF=90�㣬AC=CF���ó�A��C=CF��֤����A��CF�ǵȱ������Σ��ó���A��CF=60�㣬�����ACA�伴�ɣ�
��2��֤����A��DE=��ADC=90�㣬�ó�AD��CD�����A��D��DE���ı���CDEF�����=�ȱ�������A��CF�����-ֱ��������A��DE����������ɵó������
��� �⣺��1����ת30�㣬�������£�
����ת�����ʵã�A��C=AC����A��=��BAC=60�㣬
���ı���ACFG�������Σ�
���ACF=90�㣬AC=CF��
��A��C=CF��
�ߡ�BAC=60�㣬
���A��CF�ǵȱ������Σ�
���A��CF=60�㣬
���ACA��=90��-60��=30�㣬
����ACB������ת30����ܵõ���A��B��C��
��2���ɣ�1���ã���ACA��=30�㣬
���ACA��+��BAC=90�㣬
���A��DE=��ADC=90�㣬
��AD=$\frac{1}{2}$AC=2+$\sqrt{3}$��
��CD=$\sqrt{3}$AD=2$\sqrt{3}$+3��
��A��D=A��C-CD=1��
�ߡ�A��ED=90��-60��=30�㣬
��DE=$\sqrt{3}$A��D=$\sqrt{3}$��
���ACB���A��B��C���ص����֣����ı���CDEF�������
=�ȱ�������A��CF�����-ֱ��������A��DE�����
=$\frac{1}{2}$����4+$\sqrt{3}$����2$\sqrt{3}$+3��-$\frac{1}{2}$��1��$\sqrt{3}$
=12+$\frac{13\sqrt{3}}{2}$��
���� ���⿼������ת�����ʡ������ε����ʡ��ȱ������ε��ж������ʡ���30��ǵ�ֱ�������ε����ʣ�����������ת�����ʺ������ε����ʣ����ܽ������������ǽ������Ĺؼ���


 һ����ʦ�����Ծ�ϵ�д�
һ����ʦ�����Ծ�ϵ�д� �����Ծ���Ԫ���Ծ�ϵ�д�
�����Ծ���Ԫ���Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a=csinB | B�� | a=bcosB | C�� | c=asinB | D�� | a=btanA |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
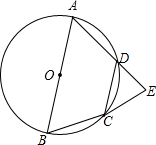 ��ͼ���ı���ABCD�ڽ��ڡ�O��AB�ǡ�O��ֱ����BC=CD��CE��AD���ӳ��ߣ�����ΪE
��ͼ���ı���ABCD�ڽ��ڡ�O��AB�ǡ�O��ֱ����BC=CD��CE��AD���ӳ��ߣ�����ΪE�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
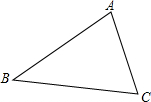 ��ͼ��һ�������εIJ˵أ�
��ͼ��һ�������εIJ˵أ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com