
【题目】如图所示,MN,EF是两面互相平行的镜面,根据镜面反射规律,若一束光线AB照射到镜面MN上,反射光线为BC,则一定有∠1=∠2.试根据这一规律:
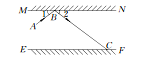
(1)利用直尺和量角器作出光线BC经镜面EF反射后的反射光线CD;
(2)试判断AB与CD的位置关系,并说明理由.
【答案】 (1)作图见解析;(2)AB∥CD.理由见解析.
【解析】试题分析:(1)根据反射光线与镜面夹角等于入射光线与镜面夹角画出即可;
(2)求出∠1=∠2=∠BCE=∠DCF,根据∠1+∠2+∠ABC=180°和∠BCE+∠DCF+∠BCD=180°推出∠ABC=∠BCD,根据平行线的判定推出即可.
试题解析:
解:(1)用量角器先量出∠BCE的度数,再在两平行镜面内作∠FCD=∠BCE(如图所示).
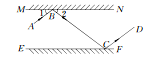
(2)AB∥CD.理由如下:
因为MN∥EF,
所以∠2=∠BCE,
根据镜面反射的规律有∠FCD=∠BCE,
所以∠1=∠2=∠BCE=∠DCF,
所以∠1+∠2=∠BCE+∠DCF,
所以180°- (∠1+∠2)=180°- (∠BCE+∠DCF),
即∠ABC=∠BCD,
所以AB∥CD.


科目:初中数学 来源: 题型:
【题目】我们规定:a*b=![]() ,则下列等式中对于任意实数 a、b、c 都成立的是( )
,则下列等式中对于任意实数 a、b、c 都成立的是( )
①a+(b*c)=(a+b)*(a+c) ②a*(b+c)=(a+b)*c
③a*(b+c)=(a*b)+(a*c) ④(a*b)+c= ![]() +(b*2c)
+(b*2c)
A. ①②③ B. ①②④ C. ①③④ D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
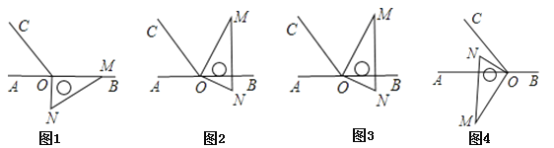
【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠AOC=60°.将一直角三角板MON的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
(1)求∠CON的度数;
(2)如图2是将图1中的三角板绕点O按每秒15°的速度沿逆时针方向旋转一周的情况,在旋转的过程中,第t秒时,三条射线OA、OC、OM构成两个相等的角,求此时的t值
(3)将图1中的三角板绕点O顺时针旋转至图3(使ON在∠AOC的外部),图4(使ON在∠AOC的内部)请分别探究∠AOM与∠NOC之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC的一角折叠,使点C落在△ABC内一点
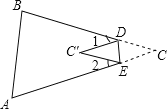
(1)若∠1=40°,∠2=30°,求∠C的度数;(2)试通过第(1)问,直接写出∠1、∠2、∠C三者之间的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中有一直角三角形AOB,O为坐标原点,OA=1,tan∠BAO=3,将此三角形绕原点O逆时针旋转90°,得到△DOC,抛物线y=ax2+bx+c经过点A,B,C.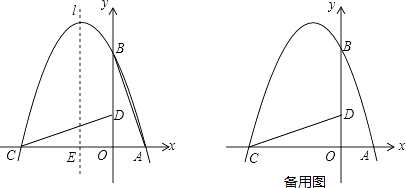
(1)求抛物线的解析式;
(2)若点P是第二象限内抛物线上的动点,其横坐标为t,
①设抛物线对称轴l与x轴交于一点E,连接PE,交CD于F,求出当△CEF与△COD相似时,点P的坐标;
②是否存在一点P,使△PCD的面积最大?若存在,求出△PCD的面积的最大值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,延长BC至点F,使CF=![]() BC,连接CD和EF.
BC,连接CD和EF.
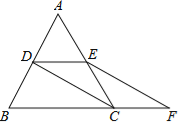
(1)求证:DE=CF;
(2)求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC=5,cos∠ABC=0.6,将△ABC绕点C顺时针旋转,得到△A1B1C.
(1)如图1,当点B1在线段BA延长线上时.①求证:BB1∥CA1;②求△AB1C的面积;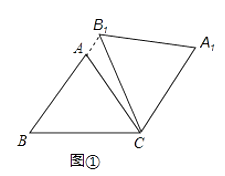
(2)如图2,点E是BC边的中点,点F为线段AB上的动点,在△ABC绕点C顺时针旋转过程中,点F的对应点是F1 , 求线段EF1长度的最大值与最小值的差.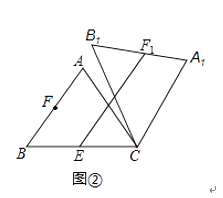
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com