
【题目】已知:如图,在△ABC、△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C、D、E三点在同一直线上,连接BD.
(1)求证:△BAD≌△CAE;
(2)请判断BD、CE有何大小、位置关系,并证明.

【答案】(1)详见解析;(2)BD=CE,BD⊥CE.
【解析】
(1)通过边角边的证明方法找出相应的边角对应关系即可.
(2)根据第一问得大小关系,再求出∠DBC+∠DCB=90°即可得位置关系.
证明:(1)∵∠BAC=∠DAE=90°,
∴∠BAC+∠CAD=∠EAD+∠CAD,
∴∠BAD=∠CAE,
在△BAD和△CAE中,
 ,
,
∴△BAD≌△CAE(SAS).
(2)BD=CE,BD⊥CE,理由如下:
由(1)知,△BAD≌△CAE,
∴BD=CE;
∵△BAD≌△CAE,
∴∠ABD=∠ACE,
∵∠ABD+∠DBC=45°,
∴∠ACE+∠DBC=45°,
∴∠DBC+∠DCB=∠DBC+∠ACE+∠ACB=90°,
则BD⊥CE.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形 ABCD 中,AB=AD,AC=5,∠DAB=∠DCB=90°, 则四边形 ABCD 的面积为( )
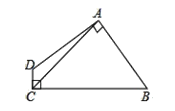
A. 15 B. 14.5 C. 13 D. 12.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2015本溪,第9题,3分)如图,在平面直角坐标系中,直线AB与x轴交于点A(﹣2,0),与x轴夹角为30°,将△ABO沿直线AB翻折,点O的对应点C恰好落在双曲线![]() (
(![]() )上,则k的值为( )
)上,则k的值为( )

A. 4 B. ﹣2 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 与双曲线
与双曲线![]() 交于
交于![]() 两点,且点
两点,且点![]() 的横坐标为
的横坐标为![]() .
.

(1)求![]() 的值;
的值;
(2)若双曲线![]() 上一点
上一点![]() 的纵坐标为8,求
的纵坐标为8,求![]() 的面积;
的面积;
(3)过原点![]() 的另一条直线
的另一条直线![]() 交双曲线
交双曲线![]() 于
于![]() 两点(
两点(![]() 点在第一象限),若由点
点在第一象限),若由点![]() 为顶点组成的四边形面积为
为顶点组成的四边形面积为![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BD平分∠ABC,AE⊥BD于点O,交BC于点E,AD∥BC,连接CD. 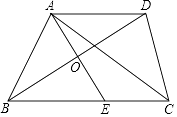
(1)求证:AO=EO;
(2)若AE是△ABC的中线,则四边形AECD是什么特殊四边形?证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣(x﹣1)2+c与x轴交于A,B(A,B分别在y轴的左右两侧)两点,与y轴的正半轴交于点C,顶点为D,已知A(﹣1,0).
(1)求点B,C的坐标;
(2)判断△CDB的形状并说明理由;
(3)将△COB沿x轴向右平移t个单位长度(0<t<3)得到△QPE.△QPE与△CDB重叠部分(如图中阴影部分)面积为S,求S与t的函数关系式,并写出自变量t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC⊥BC,AC=BC=4,以AC为直径作半圆,圆心为点O;以点C为圆心,BC为半径作 ![]() .过点O作BC的平行线交两弧于点D、E,则阴影部分的面积是 .
.过点O作BC的平行线交两弧于点D、E,则阴影部分的面积是 . 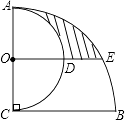
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在地面上有两根等长的立柱AB,CD,它们之间悬挂了一根抛物线形状的绳子,按照图中的直角坐标系,这条绳子可以用y= ![]() x2﹣
x2﹣ ![]() x+3表示
x+3表示 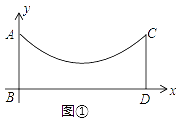
(1)求这条绳子最低点离地面的距离;
(2)现由于实际需要,要在两根立柱之间再加一根立柱EF对绳子进行支撑(如图②),已知立柱EF到AB距离为3m,两旁的绳子也是抛物线形状,且立柱EF左侧绳子的最低点到EF的距离为1m,到地面的距离为1.8m,求立柱EF的长.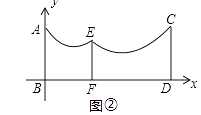
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某旅游景点的门票价格如下表:
购票人数(单位人) | 1﹣50 | 51﹣100 | 100以上 |
每人门票价(单位元) | 80 | 75 | 70 |
某旅行社计划帶甲、乙两个旅行团共100多人计划去游览该景点,其中甲旅行团人数少于50人,乙旅行团人数有50 多人但不足100人,如果两旅行团都以各自团体为单位单独购票,则一共支付7965元;如果两旅行团联合起来作为一个团体购票,则只管花费7210元.间两旅行团各有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com