
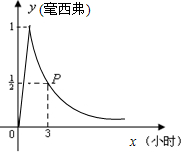
 日本大地震引发福岛核电站发生核泄漏,已知放射性物质泄漏过程中,某地每立方米空气中的辐射量y(毫西弗)与时间x(小时)成正比;后来日本抢救人员控制住了放射性物质,放射性物质不再泄漏,每立方米空气中的辐射量y与x的函数关系式为y=
日本大地震引发福岛核电站发生核泄漏,已知放射性物质泄漏过程中,某地每立方米空气中的辐射量y(毫西弗)与时间x(小时)成正比;后来日本抢救人员控制住了放射性物质,放射性物质不再泄漏,每立方米空气中的辐射量y与x的函数关系式为y=| a | x |
| a |
| x |
| 1 |
| 2 |
| a |
| x |
| 3 |
| 2 |
| 3 |
| 2x |
| 3 |
| 2x |
| 3 |
| 2 |
| 3 |
| 2x |
| 3 |
| 2 |
| 3 |
| 2 |
| k |
| x |
| 2 |
| 3 |
| 2 |
| 3 |
| 3 |
| 2 |
| 3 |
| 2x |
| 1 |
| 4 |


 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:解答题
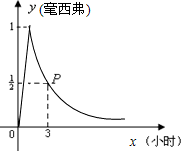 日本大地震引发福岛核电站发生核泄漏,已知放射性物质泄漏过程中,某地每立方米空气中的辐射量y(毫西弗)与时间x(小时)成正比;后来日本抢救人员控制住了放射性物质,放射性物质不再泄漏,每立方米空气中的辐射量y与x的函数关系式为
日本大地震引发福岛核电站发生核泄漏,已知放射性物质泄漏过程中,某地每立方米空气中的辐射量y(毫西弗)与时间x(小时)成正比;后来日本抢救人员控制住了放射性物质,放射性物质不再泄漏,每立方米空气中的辐射量y与x的函数关系式为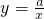 (a为常数),如图所示.据图中提供的信息,解答下列问题:
(a为常数),如图所示.据图中提供的信息,解答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com