
【题目】有大小两种货车,3辆大货车与2辆小货车一次可以运货21吨,2辆大货车与4辆小货车一次可以运货22吨.
(1)每辆大货车和每辆小货车一次各可以运货多少吨?
(2)现有这两种货车共10辆,要求一次运货不低于35吨,则其中大货车至少多少辆?(用不等式解答)
(3)日前有23吨货物需要运输,欲租用这两种货车运送,要求全部货物一次运完且每辆车必须装满.已知每辆大货车一次运货租金为300元,每辆小货车一次运货租金为200元,请列出所有的运输方案井求出最少租金.
【答案】(1)1辆大货车和1辆小货车一次可以分别运货5吨、3吨;(2)至少需要安排3辆大货车;(3)方案1:租用4辆大货车,1辆小货车;方案2:租用1辆大货车,6辆小货车;最少租金为1400元.
【解析】
(1)设1辆大货车和1辆小货车一次可以分别运货x吨、y吨,根据“3辆大货车与2辆小货车一次可以运货21吨,2辆大货车与4辆小货车一次可以运货22吨”列方程组求解可得;
(2)设安排m辆大货车,则小货车需要(10-m)辆,根据两种货车运送的货物总质量不低于35吨列一元一次不等式求解可得;
(3)设租大货车a辆,小货车b辆.根据日前有23吨货物需要运输列出不等式,结合a,b为非负整数求出a,b的值,再求出各方案所需资金,比较后即可得出结论.
解:(1)设1辆大货车和1辆小货车一次可以分别运货x吨、y吨,
根据题意,得:![]() ,
,
解得:![]() ,
,
答:1辆大货车和1辆小货车一次可以分别运货5吨、3吨.
(2)设安排m辆大货车,则小货车需要(10-m)辆,
根据题意,得:5m+3(10-m)≥35,
解得:m≥2.5,
所以至少需要安排3辆大货车;
(3)设租大货车a辆,小货车b辆,由题意得
5a+3b=23,
∵a,b为非负整数,
∴![]() 或
或![]() ,
,
∴共有2中运输方案,方案1:租用4辆大货车,1辆小货车;方案2:租用1辆大货车,6辆小货车.
方案1的租金:300×4+200=1400元,
方案2的租金:300+200×6=1500元,
∵1400<1500,
∴最少租金为1400元.


科目:初中数学 来源: 题型:
【题目】体育老师对九年级(9)班50位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图.如下所示:
组别 | 次数x | 频数(人数) |
第1组 | 80≤x<100 | 6 |
第2组 | 100≤x<120 | 8 |
第3组 | 120≤x<140 | a |
第4组 | 140≤x<160 | 18 |
第5组 | 160≤x<180 | 6 |

请结合图表完成下列问题:
(1)表中的a=________;
(2)请把频数分布直方图补充完整;
(3)这个样本数据的中位数落在第________组;
(4)若九年级学生一分钟跳绳次数(x)达标要求是:x<120为不合格;120≤x<140,为合格;140≤x<160为良;x≥160为优.根据以上信息,请你给学校或九年级同学提一条合理化建议:_________________________________________________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①,D是等边△ABC的边BA上一动点(点D与点B不重合),连接DC,以DC为边,在BC上方作等边△DCF,连接AF,你能发现AF与BD之间的数量关系吗?并证明你发现的结论;
(2)如图②,当动点D运动至等边△ABC边BA的延长线时,其他作法与(1)相同,猜想AF与BD在(1)中的结论是否仍然成立?若成立,请证明;
(3)Ⅰ.如图③,当动点D在等边△ABC边BA上运动时(点D与B不重合),连接DC,以DC为边在BC上方和下方分别作等边△DCF和等边△DCF′,连接AF,BF′,探究AF,BF′与AB有何数量关系?并证明你的探究的结论;
Ⅱ.如图④,当动点D在等边△ABC的边BA的延长线上运动时,其他作法与图③相同,Ⅰ中的结论是否成立?若不成立,是否有新的结论?并证明你得出的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC 中,AB=AC,D 是直线 BC 上一点(不与点 B、C 重合),以 AD 为一边在 AD的右侧作△ADE,AD=AE,∠DAE=∠BAC,连接 CE.
(1)如图 1,当点 D 在线段 BC 上时,求证:△ABD≌△ACE;
(2)如图 2,当点 D 在线段 BC 上时,如果∠BAC=90°,求∠BCE 的度数;
(3)如图 3,若∠BAC=α,∠BCE=β.点 D 在线段 CB 的延长线上时,则α、β之间有怎样 的数量关系?并证明你的结论.



查看答案和解析>>
科目:初中数学 来源: 题型:
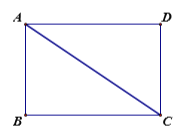
【题目】已知,如图:一张矩形纸片![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 边上一动点,将矩形沿
边上一动点,将矩形沿![]() 折叠,要使点
折叠,要使点![]() 落在
落在![]() 上,则折痕
上,则折痕![]() 的长度是________;若点
的长度是________;若点![]() 落在
落在![]() 上,则折痕
上,则折痕![]() 与
与![]() 的位置关系是__________.若翻折后
的位置关系是__________.若翻折后![]() 点的对应点是
点的对应点是![]() 点,连接
点,连接![]() ,则在点
,则在点![]() 运动的过程中,
运动的过程中,![]() 的最小值是______.
的最小值是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作
交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作![]() ,垂足为D.
,垂足为D.

(1)求证:CD为⊙O的切线;
(2)若DC+DA=6,⊙O的直径为10,求AB的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,反比例函数y= ![]() 的图象与一次函数y=x+b的图象交
的图象与一次函数y=x+b的图象交
于点A(1,4)、点B(-4,n).

(1)求一次函数和反比例函数的解析式;
(2)求△OAB的面积;
(3)直接写出一次函数值大于反比例函数值的自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,半径均为1个单位长度的半圆O1,O2,O3,… 组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒![]() 个单位长度,则第2019秒时,点P的坐标是________________
个单位长度,则第2019秒时,点P的坐标是________________

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com