
【题目】如图,一次函数y=kx+1(k≠0)与反比例函数y= ![]() (m≠0)的图象有公共点A(1,2).直线l⊥x轴于点N(3,0),与一次函数和反比例函数的图象分别交于点B,C.
(m≠0)的图象有公共点A(1,2).直线l⊥x轴于点N(3,0),与一次函数和反比例函数的图象分别交于点B,C. 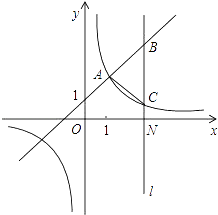
(1)求一次函数与反比例函数的解析式;
(2)求△ABC的面积?
【答案】
(1)解:将A(1,2)代入一次函数解析式得:k+1=2,即k=1,
∴一次函数解析式为y=x+1;
将A(1,2)代入反比例解析式得:m=2,
∴反比例解析式为y= ![]()
(2)解:∵N(3,0),
∴点B横坐标为3,
将x=3代入一次函数得:y=4,将x=3代入反比例解析式得:y= ![]() ,
,
即CN= ![]() ,BC=4﹣
,BC=4﹣ ![]() =
= ![]() ,A到BC的距离为:2,
,A到BC的距离为:2,
则S△ABC= ![]() ×
× ![]() ×2=
×2= ![]()
【解析】(1)将A坐标代入一次函数解析式中求出k的值,确定出一次函数解析式,将A坐标代入反比例函数解析式中求出m的值,即可确定出反比例解析式;(2)直接求出BN,CN的长,进而求出BC的长,即可求出△ABC的面积.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】小芳同学有两根长度为4cm、10cm的木棒,她想钉一个三角形相框,桌上有五根木棒供她选择(如图所示),从中任选一根,能钉成三角形相框的概率是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点A是x轴正半轴上的动点,点B坐标为(0,4),M是线段AB的中点,将点M绕点A顺时针方向旋转90°得到点C,过点C作x轴的垂线,垂足为F,过点B作y轴的垂线与直线CF相交于点E,点D是点A关于直线CF的对称点,连结AC,BC,CD,设点A的横坐标为t.
(1)当t=2时,求CF的长;
(2)①当t为何值时,点C落在线段BD上;
②设△BCE的面积为S,求S与t之间的函数关系式;
(3)如图2,当点C与点E重合时,将△CDF沿x轴左右平移得到△C′D′F′,再将A,B,C′,D′为顶点的四边形沿C′F′剪开,得到两个图形,用这两个图形拼成不重叠且无缝隙的图形恰好是三角形.请直接写出所有符合上述条件的点C′的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末,老师带同学去北京植物园中的一二﹒九运动纪念广场,这里有三座侧面为三角形的纪念亭,挺拔的建筑线条象征青年朝气蓬勃、积极向上的精神.基于纪念亭的几何特征,同学们编拟了如下的数学问题:

如图1,点A,B,C,D在同一条直线上,在四个论断“EA=ED,EF⊥AD,AB=DC,FB=FC”中选择三个作为已知条件,另一个作为结论,构成真命题(补充已知和求证),并进行证明.
已知:如图,点A,B,C,D在同一条直线上, .
求证: .
证明: .
查看答案和解析>>
科目:初中数学 来源: 题型:
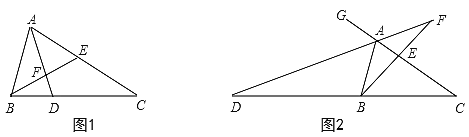
【题目】如图,在△ABC中,点E在AC上,∠AEB=∠ABC.
(1)图1中,作∠BAC的角平分线AD,分别交CB、BE于D、F两点,求证:∠EFD=∠ADC;
(2)图2中,作△ABC的外角∠BAG的角平分线AD,分别交CB、BE的延长线于D、F两点,试探究(1)中结论是否仍成立?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形ABCD是矩形,AD∥x轴,A(﹣ ![]() ,3 ),AB=2,AD=3.
,3 ),AB=2,AD=3. 
(1)直接写出B、C、D三点的坐标;
(2)将矩形ABCD向右平移m个单位,使点A、C恰好同时落在反比例函数y= ![]() (x>0)的图象上,得矩形A'B'C'D'.求矩形ABCD的平移距离m和反比例函数的解析式.
(x>0)的图象上,得矩形A'B'C'D'.求矩形ABCD的平移距离m和反比例函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点P是抛物线:y=x2上的动点(点在第一象限内).连接 OP,过点0作OP的垂线交抛物线于另一点Q.连接PQ,交y轴于点M.作PA丄x轴于点A,QB丄x轴于点B.设点P的横坐标为m.
(1)如图1,当m= ![]() 时,
时,
①求线段OP的长和tan∠POM的值;
②在y轴上找一点C,使△OCQ是以OQ为腰的等腰三角形,求点C的坐标;
(2)如图2,连接AM、BM,分别与OP、OQ相交于点D、E.
①用含m的代数式表示点Q的坐标;
②求证:四边形ODME是矩形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com