
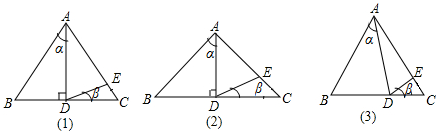
分析 (1)等腰三角形三线合一,所以∠α=35°,又因为AD=AE,所以∠ADE=∠AED=$\frac{145°}{2}$,所以∠β=$\frac{35°}{2}$°;
(2)同理,易证∠ADE=67°,所以∠β=23°;
(3)由于AD=AE,所以∠ADE=∠AED,根据已知,易证∠α+∠B=2∠β+∠C,而∠B=∠C,所以∠α=2∠β.
解答 解解:(1)∵在△ABC中,AB=AC,AD是BC上的高,
∴∠α=∠CAD,
∵∠α=35°,
∴∠α=∠CAD=35°,
∵AD=AE,
∴∠ADE=∠AED=$\frac{145°}{2}$,
∴∠β=90°-$\frac{145°}{2}$=$\frac{35°}{2}$;
故答案为:$\frac{35°}{2}$;
(2)∵在△ABC中,AB=AC,AD是BC上的高,
∴∠α=∠CAD,
∵∠α=46°,
∴∠BAD=∠CAD=46°,
∵AD=AE,
∴∠ADE=∠AED=67°,
∴∠β=23°;
故答案为:23°;
(3)∵AD=AE,
∴∠ADE=∠AED,
∴∠α+∠B=∠ADC=∠ADE+∠β=∠AED+∠β=(∠β+∠C)+∠β=2∠EDC+∠C
又∵AB=AC,
∴∠B=∠C,
∴∠α=2∠β.
点评 本题考查了等腰三角形三线合一的性质,等边对等角的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记性质是解题的关键.


科目:初中数学 来源: 题型:解答题
 在数轴上表示下列各数并按从小到大的顺序用“<”把这些数连接起来.
在数轴上表示下列各数并按从小到大的顺序用“<”把这些数连接起来.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m≥1 | B. | m≥1且m≠2 | C. | m≤1且m≠2 | D. | m≤1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com