
【题目】探究与发现:在△ABC中,∠B=∠C,点D在BC边上(点B、C除外),点E在AC边上,且∠ADE=∠AED,连接DE.
(1)如图①,若∠B=∠C=45,
①当∠BAD=60时,求∠CDE的度数;
②试猜想∠BAD与∠CDE的数量关系,并说明理由.
(2)深入探究:如图②,若∠B=∠C,但∠C≠45,其他条件不变,试探究∠BAD与∠CDE的数量关系.

【答案】(1)①∠CDE=30°;②∠BAD=2∠CDE,理由见解析;(2)∠BAD=2∠CDE.
【解析】
(1)①先根据三角形外角的性质得出∠ADC=∠B+∠BAD=105°,∠AED=∠EDC=75°,再由∠CDE=∠ADC-∠ADE即可得出结论;
②引入参数,设∠BAD=x,根据①的过程方法解答即可
(2)同(1)理,用角直接计算进行转化即可.
解:(1)①∵∠ADC是△ABD的外角,∠B=45°,∠BAD=60°,
∴∠ADC=∠BAD+∠B=60°+45°=105°,
∵∠B=∠C=45,
∴∠BAC=90°,
∠DAE=∠BAC﹣∠BAD=90°-60°=30°,
∴∠ADE=∠AED=![]() =
=![]() = 75°,
= 75°,
∴∠CDE=∠ADC-∠ADE =105°﹣75°=30°;
②∠BAD=2∠CDE,
理由如下:设∠BAD=x,
∴∠ADC=∠BAD+∠B=45°+x,
∵∠B=∠C=45,
∴∠BAC=90°,
∴∠DAE=∠BAC﹣∠BAD=90°﹣x,
∴∠ADE=∠AED=![]() =
=![]() ,
,
∴∠CDE=∠ADC-∠ADE =45°+x﹣![]() =
=![]() x,
x,
∴∠BAD=2∠CDE;
(2)设∠BAD=x,
∴∠ADC=∠BAD+∠B=∠B+x,
∵∠B=∠C,
∴∠BAC=180°﹣2∠C,
∴∠DAE=∠BAC﹣∠BAD=180°﹣2∠C﹣x,
∴∠ADE=∠AED=![]() =
=![]() =∠C+
=∠C+![]() x,
x,
∴∠CDE=∠ADC-∠ADE=(∠B+x)﹣(∠C+![]() x)=
x)=![]() x,
x,
∴∠BAD=2∠CDE.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
【题目】如图所示,四边形ABCD是正方形,E是CD的中点,P是BC边上的一点,下列条件:![]() ;
;![]() ;
;![]() 是BC的中点;
是BC的中点;![]() :
:![]() :3,其中能推出
:3,其中能推出![]() ∽
∽![]() 的有
的有![]()
![]()

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
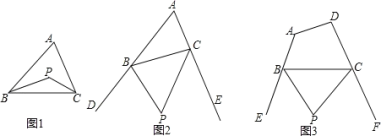
【题目】(1)探究1:如图1,P是△ABC的内角∠ABC与∠ACB的平分线BP和CP的交点,若∠A=70,则∠BPC=_______度;
(2)探究2:如图2,P是△ABC的外角∠DBC与外角∠ECB的平分线BP和CP的交点,求∠BPC与∠A的数量关系?并说明理由。
(3)拓展:如图3,P是四边形ABCD的外角∠EBC与∠BCF的平分线BP和CP的交点,设∠A+∠D=α.,直接写出∠BPC与α的数量关系;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A、F、E、C在同一直线上,AB∥CD,∠ABE=∠CDF,AF=CE.
(1)从图中任找两组全等三角形;
(2)从(1)中任选一组进行证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是边长为6cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC匀速运动,其中点P运动的速度是1cm/s,点Q运动的速度是2cm/s,当点Q到达点C时,P、Q两点都停止运动,设运动时间为t(s),解答下列问题:
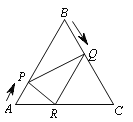
(1)当t=2时,判断△BPQ的形状,并说明理由;
(2)设△BPQ的面积为S(cm2),求S与t的函数关系式;
(3)作QR//BA交AC于点R,连结PR,当t为何值时,△APR∽△PRQ?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】经测算,某地气温![]() 与距离地面的高度
与距离地面的高度![]() 有如下对应关系:
有如下对应关系:
| 0 | 1 | 2 | 3 | 4 | 5 | … |
| 26 | 20 | 14 | 8 |
| -4 | … |
请根据上表,完成下面的问题.
(1)猜想:距离地面的高度每上升![]() ,气温就下降______
,气温就下降______![]() ;表中
;表中![]() ______.
______.
(2)气温![]() 与高度
与高度![]() 之间的函数关系式是______.
之间的函数关系式是______.
(3)求该地距离地面![]() 处的气温.
处的气温.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在口ABCD中,AB⊥AC,AB=1,BC=![]() ,对角线BD、AC交于点O.将直线AC绕点O顺时针旋转分别交BC、AD于点E、F.
,对角线BD、AC交于点O.将直线AC绕点O顺时针旋转分别交BC、AD于点E、F.

(1)试说明在旋转过程中,AF与CE总保持相等;
(2)证明:当旋转角为90时,四边形ABEF是平行四边形;
(3)在旋转过程中,四边形BEDF可能是菱形吗?如果不能,请说明理由;如果能,求出此时AC绕点O顺时针旋转的角度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于频率与概率有下列几种说法:( )
①“明天下雨的概率是90%”表示明天下雨的可能性很大;
②“抛一枚硬币正面朝上的概率为![]() ”表示每抛两次就有一次正面朝上;
”表示每抛两次就有一次正面朝上;
③“某彩票中奖的概率是1%”表示买10张该种彩票不可能中奖;
④“抛一枚硬币正面朝上的概率为![]() ”表示随着抛掷次数的增加,“抛出正面朝上”这一事件发生的频率稳定在
”表示随着抛掷次数的增加,“抛出正面朝上”这一事件发生的频率稳定在![]() 附近,正确的说法是
附近,正确的说法是
A.①④ B.②③ C.②④ D.①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:
①4ac<b2;②方程ax2+bx+c=0的两个根是x1=﹣1,x2=3;
③3a+c=0;④当y>0时,x的取值范围是﹣1≤x<3;⑤当x<0时,y随x增大而增大,其中结论正确的是_____(只需填序号)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com