
分析 (1)利用每天保存该批产品的费用乘以x即可;
(2)设批发商在保存该批产品x(x≤15)天时一次性卖出,获利W元,用总利润等于总销售额分别减去保存费用、总成本得到W=(700-15x)•y-50x-40×700,再把y=50+2x代入得到W与x的二次函数关系式,利用配方法得到W=-30(x-10)2+10000,然后根据二次函数的最值问题求解.
解答 解:(1)因为批发商每天保存该批产品的费用为50元,
所以保存该批产品的费用为50x元;
故答案为50x;
(2)设批发商在保存该批产品x(x≤15)天时一次性卖出,获利W元,
根据题意得W=(700-15x)•y-50x-40×700
=(700-15x)•(50+2x)-50x-40×700
=-30x2+600x+7000
=-30(x-10)2+10000,
∵x≤15,
∴当x=10时,W有最大值,最大值为10000,
即批发商应在保存该批产品10天时一次性卖出可获利最多,最多获利10000元.
点评 本题考查了二次函数的应用:利用二次函数解决利润问题,在商品经营活动中,经常会遇到求最大利润,最大销量等问题.解此类题的关键是通过题意,确定出二次函数的解析式,然后确定其最大值,实际问题中自变量x的取值要使实际问题有意义,因此在求二次函数的最值时,一定要注意自变量x的取值范围.


科目:初中数学 来源: 题型:解答题
 如图所示,折线ABC是在某市乘出租车需付车费y(元)与行车里程x(千米)之间的函数关系图象.若某人付费30.8元,出租车行驶了多少千米?
如图所示,折线ABC是在某市乘出租车需付车费y(元)与行车里程x(千米)之间的函数关系图象.若某人付费30.8元,出租车行驶了多少千米?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
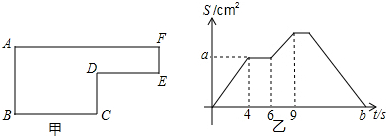
| A. | 图1中BC的长是4厘米 | B. | 图2中的a是12 | ||
| C. | 图1中的图形面积是60平方厘米 | D. | 图2中的b是19 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
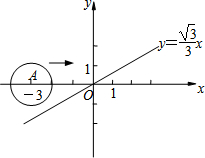 如图,在平面直角坐标系中,x轴上一点A从点(-3,0)出发沿x轴向右平移,当以A为圆心,半径为1的圆与函数y=$\frac{\sqrt{3}}{3}$x的图象相切时,点A的坐标变为( )
如图,在平面直角坐标系中,x轴上一点A从点(-3,0)出发沿x轴向右平移,当以A为圆心,半径为1的圆与函数y=$\frac{\sqrt{3}}{3}$x的图象相切时,点A的坐标变为( )| A. | (-2,0) | B. | (-$\sqrt{3}$,0)或($\sqrt{3}$,0) | C. | (-$\sqrt{3}$,0) | D. | (-2,0)或(2,0) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 我们知道平行四边形有很多性质,现在如果我们把平行四边形沿着它的一条对角线翻折,会发现这其中还有更多的结论.
我们知道平行四边形有很多性质,现在如果我们把平行四边形沿着它的一条对角线翻折,会发现这其中还有更多的结论.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com