
【题目】一次函数y=kx+b图象经过点(1,3)和(4,6)
①试求![]() 与
与![]() ;
;

②画出这个一次函数图象;
③这个一次函数与y轴交点坐标是( )
④当x 时,y<0.
【答案】(1)k=1,b=2;(2)答案见解析;(3)(0,2);(4)x<﹣2.
【解析】
①把点(1,3)和(4,6)代入一次函数y=kx+b中可得关于k、b的方程组,再解方程组即可得到k、b的值;
②根据k、b的值可得函数解析式,然后过(﹣2,0)和(0,2)画直线即可;
③一次函数与y轴交点坐标就是x=0时,计算自变量y的值,进而得到交点坐标;
④当x=﹣2时,y=0,再由图像可直接得到答案.
①∵一次函数y=kx+b的图象经过点(1,3)和(4,6),∴![]() ,解得:
,解得:![]() ;
;
②函数解析式为y=x+2,如图所示:
③当x=0时,y=2,这个一次函数与y轴交点坐标是(0,2);
④当x=﹣2时,y=0,由图像可知:当x<﹣2时,y<0.


科目:初中数学 来源: 题型:
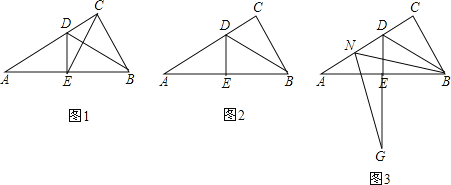
【题目】在Rt△ABC中,∠ACB=90°,∠A=30°,BD是△ABC的角平分线,DE⊥AB于点E.
(1)如图1,连接EC,求证:△EBC是等边三角形;
(2)点M是线段CD上的一点(不与点C,D重合),以BM为一边,在BM的下方作∠BMG=60°,MG交DE延长线于点G.求证:AD=DG+MD;
(3)点N是线段AD上的一点,以BN为一边,在BN的下方作∠BNG=60°,NG交DE延长线于点G.请在图3中画出图形,并直接写出ND,DG与AD数量之间的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
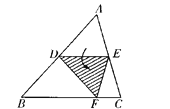
【题目】如图,点D为边AB的中点,DE∥BC,将△ABC沿线段DE折叠,使点A落在点F处,若∠B=50°,则∠EDF=_______,∠BDF=_______,若AB=10cm,则FD= ________cm。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①:在四边形ABCD中,AB=AD,∠BAD=120°,∠B=ADC=90°,E、F分别是BC,CD上的点,且∠EAF=60°,探究图中线段BE,EF,FD之间的数量关系。
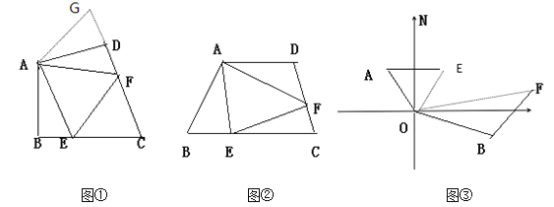
(1)小王同学探究此问题的方法是:延长FD到点G,使DG=BE,连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,即可得出BE,EF,FD之间的数量关系,他的结论应是____________。
象上面这样有公共顶点,锐角等于较大角的一半,且组成这个较大角的两边相等的几何模型称为半角模型。
(2)拓展 如图②,若在四边形ABCD中,,AB=AD,∠B+∠D=180°,E、F分别是BC,CD上的点,且∠EAF=![]() ∠BAD,则BE,EF,FD之间的数量关系是________________。
∠BAD,则BE,EF,FD之间的数量关系是________________。
请证明你的结论。
(3)实际应用 如图③,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西35°的A处,舰艇乙在指挥中心南偏东75°的B处,,且两舰艇到指挥中心的距离相等接到行动指令后,舰艇甲向正东方向以60海里/小时的速度前进,舰艇乙沿北偏东50°的方向以80海里小时的速度前进,1.2小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇之间的夹角为65°,试求此时两舰艇之间的距离是_____________海里 (直接写出答案)。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)![]() = ; (2)
= ; (2)![]() = ; (3)
= ; (3)![]() ;
;
(4)![]() ; (5)
; (5)![]() ; (6)a3·a3= ;
; (6)a3·a3= ;
(7) (x3)5= ; (8)(-2x2y3)3= ; (9) (x-y)6÷(x-y)3= ;
(10)a2b(ab-4b2) (11)(2a-3b)(2a+5b)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,AB=15,BC=9,点P,Q分别在BC,AC上,CP=3x,CQ=4x(0<x<3).点D在线段PQ上,且PD=PC. 
(1)求证:PQ∥AB;
(2)若点D在∠BAC的平分线上,求CP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
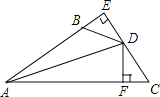
【题目】如图,DE⊥AB于E,DF⊥AC于F,若BD=CD、BE=CF,
(1)求证:AD平分∠BAC;
(2)已知AC=20,AB=12,求CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+4x﹣k=0有两个不相等的实数根.
(1)求k的取值范围;
(2)请你在﹣5,﹣4,﹣3,1,2,3中选择一个数作为k的值,使方程有两个整数根,并求出方程的两个整数根.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com