
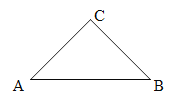
【题目】如图,在△ABC中,∠ACB=90°,AC=BC=4.
(1)尺规作图:将△ABC绕AC的中点O为旋转180°,点B的对应点为B′(保留作图痕迹,不写做法);
(2)求点B与点B′之间的距离.
【答案】(1)作图见解析;(2)4![]() .
.
【解析】
(1)先作出AC的中点O,再根据图形旋转的性质画出旋转后的图形即可;
(2)先根据勾股定理求出OB的长,再由旋转的性质求出OB′的长,进而可得出结论.
(1)作线段AC的垂直平分线EF,EF交AC于点O,则O为线段AC的中点,作射线BO,以O为圆心,OB为半径作⊙O交射线BO于B和B′,连接AB′,CB′.则△AB′C就是△ABC绕点O旋转180°后得到的三角形;
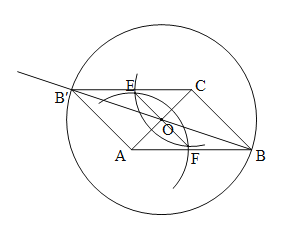
(2)∵点O是AC边中点,∴OC=![]() AC=2.
AC=2.
∵∠ACB=90°,∴OB=![]() =
=![]() =
=![]() .
.
∵△ABC绕AC中点O旋转180°得到△AB′C,∴点B,O,B′在同一直线上,OB′=OB=![]() ,∴BB′=
,∴BB′=![]() ,即点B与点B′之间的距离为
,即点B与点B′之间的距离为![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
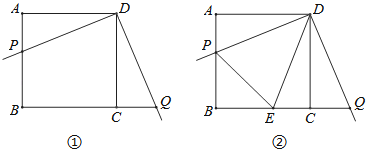
【题目】某校数学兴趣小组开展了一次课外活动,过程如下:如图①,正方形ABCD中,AB=4,将三角板放在正方形ABCD上,使三角板的直角顶点与D点重合.三角板的一边交AB于点P,另一边交BC的延长线于点Q.
(1)求证:AP=CQ;
(2)如图②,小明在图1的基础上作∠PDQ的平分线DE交BC于点E,连接PE,他发现PE和QE存在一定的数量关系,请猜测他的结论并予以证明;
(3)在(2)的条件下,若AP=1,求PE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市射击队甲、乙两名队员在相同的条件下各射耙10次,每次射耙的成绩情况如图所示:
(1)请将下表补充完整:(参考公式:方差S2=![]() [(x1﹣
[(x1﹣![]() )2+(x2﹣
)2+(x2﹣![]() )2+…+(xn﹣
)2+…+(xn﹣![]() )2])
)2])
平均数 | 方差 | 中位数 | |
甲 | 7 |
| 7 |
乙 |
| 5.4 |
|
(2)请从下列三个不同的角度对这次测试结果进行
①从平均数和方差相结合看, 的成绩好些;
②从平均数和中位数相结合看, 的成绩好些;
③若其他队选手最好成绩在9环左右,现要选一人参赛,你认为选谁参加,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
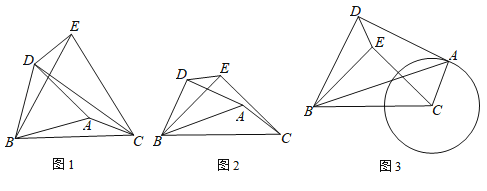
【题目】已知两条线段AC和BC,连接AB,分别以AB、BC为底边向上画等腰△ABD和等腰△BCE,∠ADB=∠BEC=α.
(1)如图1,当α=60°时,求证:△DBE≌△ABC;
(2)如图2,当α=90°时,且BC=5,AC=2.
①求DE的长;
②如图3,将线段CA绕点C旋转,点D也随之运动,请求出C,D两点之间距离的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c的顶点为A(﹣3,3),且与y轴交于点B(0,5),若平移该抛物线,使其顶点A沿y=﹣x由(﹣3,3)移动到(2,﹣2),此时抛物线与y轴交于点B′,则BB′的长度为________.
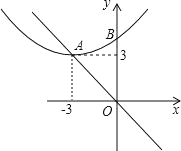
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,不正确的是( )
A. 直角边长分别是6、4和4.5、3的两个直角三角形相似 B. 底角为40°的两个等腰三角形相似
C. 一个锐角为30°的两个直角三角形相似 D. 有个角为30°的两个等腰三角形相似
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连接BD、DP,BD与CF相交于点H,给出下列结论:
①BE=2AE;②△DFP∽△BPH;③△PFD∽△PDB;④DP2=PHPC
其中正确的是_____(填序号)
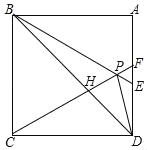
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场将进价为2000元的冰箱以2400元售出,平均每天能售出8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调查表明:这种冰箱的售价每降低50元,平均每天就能多售出 4台.商场要想在这种冰箱销售中每天盈利 4800 元,同时又要使百姓得到实惠,每台冰箱应降价多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com