
【题目】在全市中学运动会800m比赛中,甲、乙两名运动员同时起跑,刚跑出200m后,甲不慎摔倒,他又迅速地爬起来继续投入比赛,并取得了优异的成绩.图中分别表示甲、乙两名运动员所跑的路程y(m)与比赛时间x(s)之间的关系,根据图象解答下列问题:

(1)甲再次投入比赛后,甲的速度为;
(2)甲再次投入比赛后,在距离终点多远处追上乙?
【答案】(1)4m/s;(2)甲在距离终点200m处追上乙.
【解析】
(1)根据函数图象中的数据可以计算出甲再次投入比赛后,甲的速度;
(2)根据函数图象中的数据可以求得乙对应的函数解析式,然后即可求得甲乙相遇的时刻,从而可以计算出甲再次投入比赛后,在距离终点多远处追上乙.
解:(1)由图象可得,
甲再次投入比赛后,甲的速度为:(800200)÷(250100)=600÷150=4(m/s),
故答案为:4m/s;
(2)设乙对应的函数解析式为y=kx,
![]() k=800,得k=3,
k=800,得k=3,
即乙对应的函数解析式为y=3x,
令3x=200+4(x100),得x=200,
故甲再次投入比赛后,甲追上乙时,距离终点的距离是:8003×200=200(m),
即甲再次投入比赛后,在距离终点200m处追上乙.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,直线AB交x轴于点A(a,0),交y轴于点B(0,b),且a、b满足![]() .
.
(1)点A的坐标为 ;点B的坐标为 ;
(2)如图1,若点C的坐标为(-3,-2),且BE⊥AC于点E,OD⊥OC交BE延长线于D,试求点D的坐标;
(3)如图2,M、N分别为OA、OB边上的点,OM=ON,OP⊥AN交AB于点P,过点P 作PG⊥BM,交AN的延长线于点G,请写出线段AG、OP与PG之间的数量关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
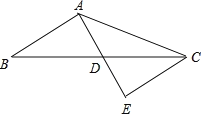
【题目】如图,在△ABC中,AB=6,AC=10,AD是BC边上的中线,且AD=4,延长AD到点E,使DE=AD,连接CE.
(1)求证:△AEC是直角三角形.
(2)求BC边的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】仔细想一想,完成下面的说理过程.
如图,已知AB∥CD,∠B=∠D
求证:∠E=∠DFE.
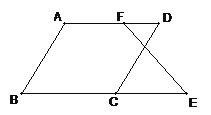
证明:∵AB∥CD (已知 ),
∴∠B+∠ =180°( )
又∵∠B=∠D(已知 )
∴∠D +∠BCD=180°( )
∴ ( )
∴∠E=∠DFE( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读短文,解决问题
如果一个三角形和一个菱形满足条件:三角形的一个角与菱形的一个角重合,且菱形的这个角的对角顶点在三角形的这个角的对边上,则称这个菱形为该三角形的“亲密菱形”.如图1,菱形AEFD为△ABC的“亲密菱形”.
如图2,在△ABC中,以点A为圆心,以任意长为半径作弧,交AB、AC于点M、N,再分别以M、N为圆心,以大于![]() MN的长为半径作弧,两弧交于点P,作射线AP,交BC于点F,过点F作FD//AC,FE//AB.
MN的长为半径作弧,两弧交于点P,作射线AP,交BC于点F,过点F作FD//AC,FE//AB.
(1)求证:四边形AEFD是△ABC的“亲密菱形”;
(2)当AB=6,AC=12,∠BAC=45°时,求菱形AEFD的面积.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】嘉嘉同学动手剪了如图①所示的正方形与长方形卡片若干张.
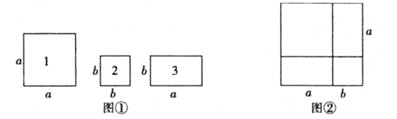
(1)他用1张1号、1张2号和2张3号卡片拼出一个新的图形(如图②).根据这个图形的面积关系写出一个你所熟悉的乘法公式,这个乘法公式是________.
(2)如果要拼成一个长为(a+2b),宽为(a+b)的大长方形,则需要1号卡片________张,2号卡片________张,3号卡片________张.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AF平分∠CAB,交CD于点E,交CB于点F.若AC=3,AB=5,则CE的长为( )
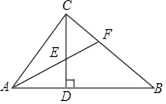
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代伟大的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式.后人借助这种分割方法所得的图形证明了勾股定理,如图所示的矩形由两个这样的图形拼成,若a=3,b=4,则该矩形的面积为( )

A. 20 B. 24 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E、F、G、H分别为矩形ABCD的边AB、BC、CD、DA的中点,连接AC、HE、EC,GA,GF.已知AG⊥GF,AC=![]() ,则AB的长为__________.
,则AB的长为__________.
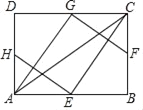
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com