
【题目】在△ABC与△ABD中,∠DBA=∠CAB,AC与BD交于点F
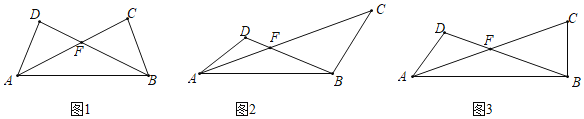
(1)如图1,若∠DAF=∠CBF,求证:AD=BC;
(2)如图2,∠D=135°,∠C=45°,AD=2,AC=4,求BD的长.
(3)如图3,若∠DBA=18°,∠D=108°,∠C=72°,AD=1,直接写出DB的长.
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两个草莓采摘园为吸引顾客,在草莓销售价格相同的基础上分别推出优惠方案,甲园:顾客进园需购买门票,采摘的草莓按六折优惠.乙园:顾客进园免门票,采摘草莓超过一定数量后,超过的部分打折销售.活动期间,某顾客的草莓采摘量为x kg,若在甲园采摘需总费用y1元,若在乙园采摘需总费用y2元, y1,y2与x之间的函数图象如图所示,则下列说法中错误的是( )
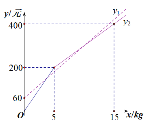
A.甲园的门票费用是60元
B.草莓优惠前的销售价格是40元/kg
C.乙园超过5 kg后,超过的部分价格优惠是打五折
D.若顾客采摘12 kg草莓,那么到甲园或乙园的总费用相同
查看答案和解析>>
科目:初中数学 来源: 题型:
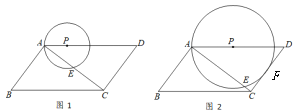
【题目】如图1,平行四边形ABCD中,AB⊥AC,AB=3,AD=5,点P在边AD上运动,以P为圆心,PA为半径的⊙P与对角线AC交于A,E两点.
(1)如图2,当⊙P与边CD相切于点F时,求AP的长;
(2)不难发现,当⊙P与边CD相切时,⊙P与平行四边形ABCD的边有三个公共点,随着AP的变化,⊙P与平行四边形ABCD的边的公共点的个数也在变化,若公共点的个数为4,直接写出相对应的AP的值的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
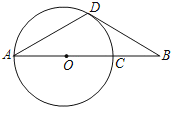
【题目】如图,线段AB经过⊙O的圆心O,交⊙O于A、C两点,BC=1,AD为⊙O的弦,连结BD,∠BAD=∠ABD=30°.
(1)求证:直线BD是⊙O的切线;
(2)求⊙O的半径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】只有1和它本身两个因数且大于1的正整数叫做素数.我国数学家陈景润哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于2的偶数都表示为两个素数的和”,如10=3+7.
(1)从7,11,13,17这4个素数中随机抽取一个,则抽到的数是11的概率是_____;
(2)从7,11,13,17这4个素数中随机抽取1个数,再从余下的3个数中随机抽取1个数,用画树状图或列表的方法,求抽到的两个素数之和等于24的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A(-1.5,0),B(0,2),将△ABO顺着x轴的正半轴无滑动的滚动,第一次滚动到①的位置,点B的对应点记作B1;第二次滚动到②的位置,点B1的对应点记作B2;第三次滚动到③的位置,点B2的对应点记作B3;![]() ;依次进行下去,则点B2020的坐标为__________.
;依次进行下去,则点B2020的坐标为__________.
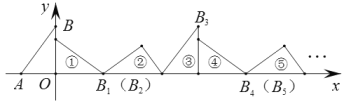
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,点
点,点![]() 在直线
在直线![]() 上,横坐标为
上,横坐标为![]() .
.
(1)确定二次函数![]() 的解析式;
的解析式;
(2)如图1,![]() 时,
时,![]() 交二次函数
交二次函数![]() 的图象于点
的图象于点![]() 的面积记作
的面积记作![]() 为何值时
为何值时![]() 的值最大,并求出
的值最大,并求出![]() 的最大值;
的最大值;
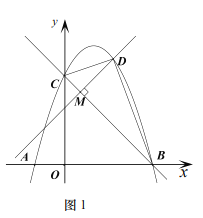
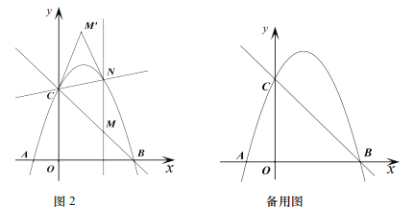
(3)如图2,过点![]() 作
作![]() 轴的平行线交二次函数
轴的平行线交二次函数![]() 的图象于点
的图象于点![]() 点
点![]() 与点
与点![]() 关于直线
关于直线![]() 对称是否存在点
对称是否存在点![]() 使四边形
使四边形![]() 为菱形,若存在直接写出
为菱形,若存在直接写出![]() 的值;若不存在请说明理由.
的值;若不存在请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com