
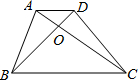
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
A.AB2=AC BC BC | B.BC2=AC AB AB | C.AC2=BC AB AB | D.AC2=2AB BC BC |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
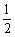 cm/s.
cm/s.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
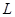 的两侧分别有观测点
的两侧分别有观测点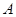 和
和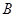 ,点
,点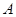 到航线
到航线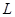 的距离为
的距离为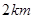 ,点
,点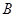 位于点
位于点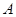 北偏东
北偏东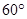 方向且与
方向且与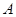 相距
相距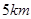 处. 现有一艘轮船正沿该航线自西向东航行,在
处. 现有一艘轮船正沿该航线自西向东航行,在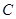 点观测到点
点观测到点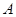 位于南偏东
位于南偏东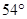 方向,航行
方向,航行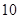 分钟后,在
分钟后,在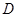 点观测到点
点观测到点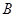 位于北偏东
位于北偏东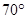 方向.
方向.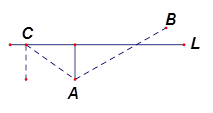
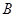 到航线
到航线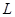 的距离;
的距离;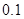 )
)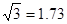 ,
,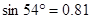 ,
,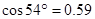 ,
,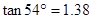 ,
,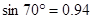 ,
,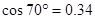 ,
,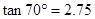 .
.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
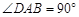 ,
, ,
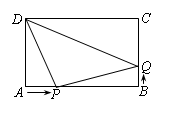
, .动点M以每秒1个单位长的速度,从点A沿线段AB向点B运动;同时点P以相同的速度,从点C沿折线C-D-A向点A运动.当点M到达点B时,两点同时停止运动.过点M作直线l∥AD,与线段CD的交点为E,与折线A-C-B的交点为Q.点M运动的时间为t(秒).
.动点M以每秒1个单位长的速度,从点A沿线段AB向点B运动;同时点P以相同的速度,从点C沿折线C-D-A向点A运动.当点M到达点B时,两点同时停止运动.过点M作直线l∥AD,与线段CD的交点为E,与折线A-C-B的交点为Q.点M运动的时间为t(秒).
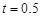 时,求线段
时,求线段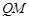 的长;
的长; 是否为定值,若是,试求这个定值;若不是,请说明理由.
是否为定值,若是,试求这个定值;若不是,请说明理由.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题



 ∶1.
∶1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com