
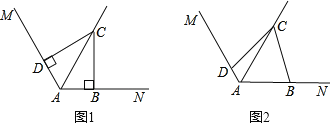
【题目】已知∠MAN=120°,AC平分∠MAN,点B、D分别在AN、AM上.
(1)如图1,若∠ABC=∠ADC=90°,请你探索线段AD、AB、AC之间的数量关系,并证明之;
(2)如图2,若∠ABC+∠ADC=180°,则(1)中的结论是否仍然成立?若成立,给出证明;若不成立,请说明理由.
【答案】(1)AD+AB=AC;(2)仍成立.
【解析】
(1)得到∠ACD=∠ACB=30°后再可以证得AD=AB![]() AC从而,证得结论;
AC从而,证得结论;
(2)过点C分别作AM、AN的垂线,垂足分别为E、F,证得△CED≌△CFB后即可得到AD+AB=AE﹣ED+AF+FB=AE+AF,从而证得结论.
(1)关系是:AD+AB=AC.证明如下:
∵AC平分∠MAN,∠MAN=120°,∴∠CAD=∠CAB=60°.
又∵∠ADC=∠ABC=90°,∴∠ACD=∠ACB=30°,则AD=AB![]() AC(直角三角形一锐角为30°,则它所对直角边为斜边一半),∴AD+AB=AC.
AC(直角三角形一锐角为30°,则它所对直角边为斜边一半),∴AD+AB=AC.
(2)仍成立.理由如下:
过点C分别作AM、AN的垂线,垂足分别为E、F.
∵AC平分∠MAN,∴CE=CF(角平分线上点到角两边距离相等).
∵∠ABC+∠ADC=180°,∠ADC+∠CDE=180°,∴∠CDE=∠ABC.
又∵∠CED=∠CFB=90°,∴△CED≌△CFB(AAS).
∵ED=FB,∴AD+AB=AE﹣ED+AF+FB=AE+AF.
由(1)知AE+AF=AC,∴AD+AB=AC.


 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y=kx+4图象交直线OA于点A(1,2),交y轴于点B,点C为坐标平面内一点.
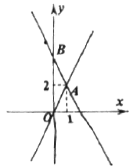
(1)求k值;
(2)若以O、A、B、C为顶点的四边形为菱形,则C点坐标为 ;
(3)在直线AB上找点D,使△OAD的面积与((2)中菱形面积相等,则D点坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=-3x与双曲线y=![]() 在第四象限内的部分相交于点A(a,-6),将这条直线向
在第四象限内的部分相交于点A(a,-6),将这条直线向
上平移后与该双曲线交于点M,且△AOM的面积为3.
(1)求k的值;
(2)求平移后得到的直线的函数表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在□ABCD中,点E在CD上,点F在AB上,连接AE、CF、DF、BE,∠DAE=∠BCF.
(1)如图1,求证:四边形DFBE是平行四边形;
(2)如图2,若E是CD的中点,连接GH,在不添加任何辅助线的情况下,请直接写出图2中以GH为边或以GH为对角线的所有平行四边形.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,点D,E分别在边AC,AB上,BD与CE交于点O,给出下列三个条件:①∠EBO=∠DCO;②
中,点D,E分别在边AC,AB上,BD与CE交于点O,给出下列三个条件:①∠EBO=∠DCO;②![]() ;③
;③![]() .
.
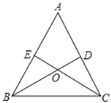
(1)上述三个条件中,由哪两个条件可以判定![]() 是等腰三角形?(用序号写出所有成立的情形)
是等腰三角形?(用序号写出所有成立的情形)
(2)请选择(1)中的一种情形,说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
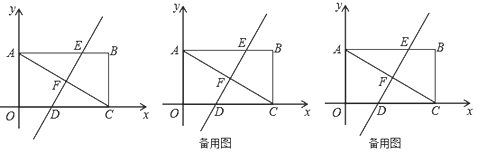
【题目】如图,平面直角坐标系中,矩形![]() 的对角线
的对角线![]() ,
,![]() .
.
(1)把矩形![]() 沿直线
沿直线![]() 对折,使点
对折,使点![]() 落在点
落在点![]() 处,折痕
处,折痕![]() 分别与
分别与![]() 、
、![]() 、
、![]() 相交于点
相交于点![]() 、
、![]() 、
、![]() ,求直线
,求直线![]() 的解析式;
的解析式;
(2)若点![]() 在直线
在直线![]() 上,平面内是否存在点
上,平面内是否存在点![]() ,使以
,使以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是菱形?若存在,请直接写出点
为顶点的四边形是菱形?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E,F是平行四边形ABCD对角线AC上两点,AE=CF=![]() AC.连接DE,DF并延长,分别交AB,BC于点G,H,连接GH,则
AC.连接DE,DF并延长,分别交AB,BC于点G,H,连接GH,则![]() 的值为( )
的值为( )
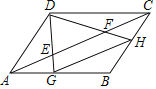
A. ![]() B.
B. ![]() C.
C. ![]() D. 1
D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
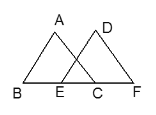
【题目】如图,已知AB∥DE,AB=DE,请你添加一个条件_______ 可以根据“ASA”使得△ABC≌△DEF;或者添加条件BE=CF,可以根据_______得到△ABC≌△DEF。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com