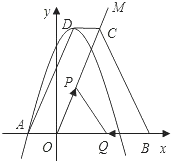
ШчЭМЃЌвбжЊХзЮяЯпy=aЃЈx-1ЃЉ
2+3
ЃЈaЁй0ЃЉОЙ§ЕуAЃЈ-2ЃЌ0ЃЉЃЌХзЮяЯпЕФЖЅЕуЮЊDЃЌЙ§OзїЩфЯпOMЁЮADЃЎЙ§ЖЅЕуЦНаагкxжсЕФжБЯпНЛЩфЯпOMгкЕуCЃЌBдкxжсе§АыжсЩЯЃЌСЌНгBCЃЎ
ЃЈ1ЃЉЧѓИУХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШєЖЏЕуPДгЕуOГіЗЂЃЌвдУПУы1ИіГЄЖШЕЅЮЛЕФЫйЖШбиЩфЯпOMдЫЖЏЃЌЩшЕуPдЫЖЏЕФЪБМфЮЊtЃЈsЃЉЃЎЮЪЕБtЮЊКЮжЕЪБЃЌЫФБпаЮDAOPЗжБ№ЮЊЦНааЫФБпаЮЃЌжБНЧЬнаЮЃЌЕШбќЬнаЮЃП
ЃЈ3ЃЉШєOC=OBЃЌЖЏЕуPКЭЖЏЕуQЗжБ№ДгЕуOКЭЕуBЭЌЪБГіЗЂЃЌЗжБ№вдУПУы1ИіГЄЖШЕЅЮЛКЭ2ИіГЄЖШЕЅЮЛЕФЫйЖШбиOCКЭBOдЫЖЏЃЌЕБЦфжавЛИіЕуЭЃжЙдЫЖЏЪБСэвЛИіЕувВЫцжЎЭЃжЙдЫЖЏЃЎЩшЫќУЧЕФдЫЖЏЕФЪБМфЮЊtЃЈsЃЉЃЌСЌНгPQЃЌЕБtЮЊКЮжЕЪБЃЌЫФБпаЮBCPQЕФУцЛ§зюаЁЃПВЂЧѓГізюаЁжЕМАДЫЪБPQЕФГЄЃЎ

 ШчЭМЃЌвбжЊХзЮяЯпy=aЃЈx-1ЃЉ2+3
ШчЭМЃЌвбжЊХзЮяЯпy=aЃЈx-1ЃЉ2+3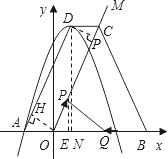



 CЃЈ0ЃЌ3ЃЉЃЎ
CЃЈ0ЃЌ3ЃЉЃЎ ЁЂCЃЈ0ЃЌ-3ЃЉСНЕуЃЌгыxжсНЛгкСэвЛЕуBЃЎ
ЁЂCЃЈ0ЃЌ-3ЃЉСНЕуЃЌгыxжсНЛгкСэвЛЕуBЃЎ ЃЈ2013•КтбєЃЉШчЭМЃЌвбжЊХзЮяЯпОЙ§AЃЈ1ЃЌ0ЃЉЃЌBЃЈ0ЃЌ3ЃЉСНЕуЃЌЖдГЦжсЪЧx=-1ЃЎ
ЃЈ2013•КтбєЃЉШчЭМЃЌвбжЊХзЮяЯпОЙ§AЃЈ1ЃЌ0ЃЉЃЌBЃЈ0ЃЌ3ЃЉСНЕуЃЌЖдГЦжсЪЧx=-1ЃЎ ШчЭМЃЌвбжЊХзЮяЯпy=ax2+bx+cЃЈaЁй0ЃЉЕФЖдГЦжсЮЊжБЯпx=1ЃЌЧвХзЮяЯпОЙ§AЃЈ-1ЃЌ0ЃЉЁЂCЃЈ0ЃЌ-3ЃЉСНЕуЃЌгыxжсНЛгкСэвЛЕуBЃЎ
ШчЭМЃЌвбжЊХзЮяЯпy=ax2+bx+cЃЈaЁй0ЃЉЕФЖдГЦжсЮЊжБЯпx=1ЃЌЧвХзЮяЯпОЙ§AЃЈ-1ЃЌ0ЃЉЁЂCЃЈ0ЃЌ-3ЃЉСНЕуЃЌгыxжсНЛгкСэвЛЕуBЃЎ ШчЭМЃЌвбжЊХзЮяЯпy=ax2+bx+cЕФЖЅЕуЪЧЃЈ-1ЃЌ-4ЃЉЃЌЧвгыxжсНЛгкAЁЂBЃЈ1ЃЌ0ЃЉСНЕуЃЌНЛyжсгкЕуCЃЛ
ШчЭМЃЌвбжЊХзЮяЯпy=ax2+bx+cЕФЖЅЕуЪЧЃЈ-1ЃЌ-4ЃЉЃЌЧвгыxжсНЛгкAЁЂBЃЈ1ЃЌ0ЃЉСНЕуЃЌНЛyжсгкЕуCЃЛ