
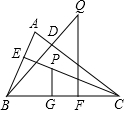
 已知:如图,在锐角△ABC中,BD,CE分别是△ABC的AC,AB边上的高,在CE上截取CP=AB,过点P作PG⊥BC于G点,在BD的延长线上截取BQ=AC,过点Q作QF⊥BC于F点,求证:PG+QF=BC.
已知:如图,在锐角△ABC中,BD,CE分别是△ABC的AC,AB边上的高,在CE上截取CP=AB,过点P作PG⊥BC于G点,在BD的延长线上截取BQ=AC,过点Q作QF⊥BC于F点,求证:PG+QF=BC. 分析 如图,作AM⊥BC于M.只要证明△PCG≌△BAM,推出PG=BM,同理可证△BQF≌△ACM,推出CM=FQ,推出PG+QF=BM+CM=BC.
解答 证明:如图,作AM⊥BC于M.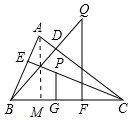
∵CE⊥AB,PG⊥BC,AM⊥BC,
∴∠AMB=∠PGC=∠CEB=90°,
∴∠BAM+∠ABM=90°,∠ABM+∠PCG=90°,
∴∠BAM=∠PCG,
在△PCG和△BAM中,
$\left\{\begin{array}{l}{∠PCG=∠BAM}\\{∠PGC=∠AMB}\\{PC=AB}\end{array}\right.$,
∴△PCG≌△BAM(AAS),
∴PG=BM,
同理可证△BQF≌△ACM,
∴CM=FQ,
∴PG+QF=BM+CM=BC.
点评 本题考查全等三角形的判定和性质,三角形的高等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,BC为⊙O的直径,A为圆上一点,点F为$\widehat{BC}$的中点,延长AB、AC,与过F点的切线交于D、E两点.
如图,BC为⊙O的直径,A为圆上一点,点F为$\widehat{BC}$的中点,延长AB、AC,与过F点的切线交于D、E两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com