
(2013年浙江义乌12分)如图1,已知 (x>
(x>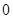 )图象上一点P,PA⊥x轴于点A(a,0),点B坐标为(0,b)(b>0),动点M是y轴正半轴上B点上方的点,动点N在射线AP上,过点B作AB的垂线,交射线AP于点D,交直线MN于点Q,连结AQ,取AQ的中点为C.
)图象上一点P,PA⊥x轴于点A(a,0),点B坐标为(0,b)(b>0),动点M是y轴正半轴上B点上方的点,动点N在射线AP上,过点B作AB的垂线,交射线AP于点D,交直线MN于点Q,连结AQ,取AQ的中点为C.

(1)如图2,连结BP,求△PAB的面积;
(2)当点Q在线段BD上时,若四边形BQNC是菱形,面积为 ,求此时P点的坐标;
,求此时P点的坐标;
(3)当点Q在射线BD上时,且a=3,b=1,若以点B,C,N,Q为顶点的四边形是平行四边形,求这个平行四边形的周长.
解:(1) 。
。
(2)如图1,∵四边形BQNC是菱形,
∴BQ=BC=NQ,∠BQC=∠NQC。
∵AB⊥BQ,C是AQ的中点,∴BC=CQ=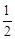 AQ。∴∠BQC=60°,∠BAQ=30°。
AQ。∴∠BQC=60°,∠BAQ=30°。
在△ABQ和△ANQ中,∵ ,∴△ABQ≌△ANQ(SAS)。
,∴△ABQ≌△ANQ(SAS)。
∴∠BAQ=∠NAQ=30°。∴∠BAO=30°。
∵S四边形BQNC= ,∴BQ=2。∴AB=
,∴BQ=2。∴AB=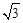 BQ=
BQ= 。∴OA=
。∴OA= AB=3。
AB=3。
又∵P点在反比例函数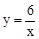 的图象上,∴P点坐标为(3,2)。
的图象上,∴P点坐标为(3,2)。
(3)∵OB=1,OA=3,∴AB= 。
。
∵△AOB∽△DBA,∴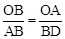 。∴BD=3
。∴BD=3 。
。
①如图2,当点Q在线段BD上,

∵AB⊥BD,C为AQ的中点,∴BC=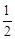 AQ。
AQ。
∵四边形BNQC是平行四边形,∴QN=BC,CN=BQ,CN∥BD。
∴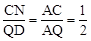 ,∴BQ=CN=
,∴BQ=CN= BD=
BD= 。
。
∴AQ=2 。
。
∴C四边形BQNC=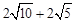 。
。
②如图3,当点Q在线段BD的延长线上,

∵AB⊥BD,C为AQ的中点,
∴BC=CQ=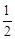 AQ。
AQ。
∴平行四边形BNQC是菱形,BN=CQ,BN∥CQ。
∴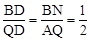 。∴BQ=3BD=9
。∴BQ=3BD=9 。
。
∴ 。
。
∴C四边形BNQC=2AQ=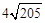 。
。
【解析】(1)根据同底等高的两个三角形的面积相等即可求出△PAB的面积。
(2)首先求出∠BQC=60°,∠BAQ=30°,然后根据SAS证明△ABQ≌△ANQ,进而求出∠BAO=30°,由S四边形BQNC= 求出OA=3,于是P点坐标求出。
求出OA=3,于是P点坐标求出。
(3)分两类进行讨论,当点Q在线段BD上,根据题干条件求出AQ的长,进而求出四边形的周长,当点Q在线段考点:反比例函数综合题,曲线上点的坐标与方程的关系,菱形的性质,全等三角形的判定和性质,相似三角形的判定和性质,勾股定理,分类思想的应用。
BD的延长线上,依然根据题干条件求出AQ的长,再进一步求出四边形的周长。


科目:初中数学 来源:2013年初中毕业升学考试(浙江义乌卷)数学(解析版) 题型:解答题
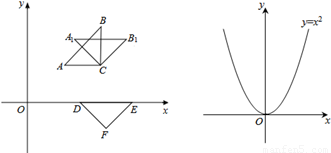
(2013年浙江义乌10分)小明合作学习小组在探究旋转、平移变换.如图△ABC,△DEF均为等腰直角三角形,各顶点坐标分别为A(1,1),B(2,2),C(2,1),D( ,0),E(
,0),E(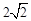 , 0),F(
, 0),F(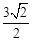 ,
,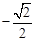 ).
).
(1)他们将△ABC绕C点按顺时针方向旋转450得到△A1B1C.请你写出点A1,B1的坐标,并判断A1C和DF的位置关系;
(2)他们将△ABC绕原点按顺时针方向旋转450,发现旋转后的三角形恰好有两个顶点落在抛物线 上.请你求出符合条件的抛物线解析式;
上.请你求出符合条件的抛物线解析式;
(3)他们继续探究,发现将△ABC绕某个点旋转45,若旋转后的三角形恰好有两个顶点落在抛物线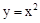 上,则可求出旋转后三角形的直角顶点P的坐标.请你直接写出点P的所有坐标.
上,则可求出旋转后三角形的直角顶点P的坐标.请你直接写出点P的所有坐标.
查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(浙江义乌卷)数学(解析版) 题型:解答题
(2013年浙江义乌10分)为迎接中国森博会,某商家计划从厂家采购A,B两种产品共20件,产品的采购单价(元/件)是采购数量(件)的一次函数.下表提供了部分采购数据.
|
采购数量(件) |
1 |
2 |
… |
|
A产品单价(元/件) |
1480 |
1460 |
… |
|
B产品单价(元/件) |
1290 |
1280 |
… |
(1)设A产品的采购数量为x(件),采购单价为y1(元/件),求y1与x的关系式;
(2)经商家与厂家协商,采购A产品的数量不少于B产品数量的 ,且A产品采购单价不低于1200元.求该商家共有几种进货方案;
,且A产品采购单价不低于1200元.求该商家共有几种进货方案;
(3)该商家分别以1760元/件和1700元/件的销售单价售出A,B两种产品,且全部售完.在(2)的条件下,求采购A种产品多少件时总利润最大,并求最大利润.
查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(浙江义乌卷)数学(解析版) 题型:解答题
(2013年浙江义乌8分)已知直线PD垂直平分⊙O的半径OA于点B,PD交⊙O于点C,D,PE是⊙O的切线,E为切点,连结AE,交CD于点F.

(1)若⊙O的半径为8,求CD的长;
(2)证明:PE=PF;
(3)若PF=13,sinA= ,求EF的长.
,求EF的长.
查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(浙江义乌卷)数学(解析版) 题型:解答题
(2013年浙江义乌8分)在义乌市中小学生“我的中国梦”读书活动中,某校对部分学生做了一次主题为“我最喜爱的图书”的调查活动,将图书分为甲、乙、丙、丁四类,学生可根据自己的爱好任选其中一类.学校根据调查情况进行了统计,并绘制了不完整的条形统计图和扇形统计图.
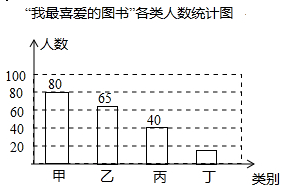

请你结合图中信息,解答下列问题:
(1)本次共调查了 名学生;
(2)被调查的学生中,最喜爱丁类图书的学生有 人,最喜爱甲类图书的人数占本次被调查人数的 %;
(3)在最喜爱丙类图书的学生中,女生人数是男生人数的1.5倍.若这所学校共有学生1500人,请你估计该校最喜爱丙类图书的女生和男生分别有多少人.
查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(浙江义乌卷)数学(解析版) 题型:解答题
(2013年浙江义乌6分)如图1,从边长为a的正方形纸片中剪去一个边长为b的小正方形,再沿着线段AB剪开,把剪成的两张纸片拼成如图2的等腰梯形.

(1)设图1中阴影部分面积为S1,图2中阴影部分面积为S2,请直接用含a,b的代数式表示S1 和S2;
(2)请写出上述过程所揭示的乘法公式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com