
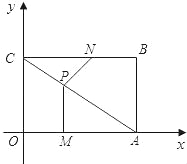
【题目】如图,平面直角坐标系中,四边形OABC为矩形,点A,B的坐标分别为(4,0),(4,3),动点M,N分别从O,B同时出发.以每秒1个单位的速度运动.其中,点M沿OA向终点A运动,点N沿BC向终点C运动.过点M作MP⊥OA,交AC于P,连接NP,已知动点运动了x秒.
(1)P点的坐标为多少(用含x的代数式表示);
(2)试求△NPC面积S的表达式,并求出面积S的最大值及相应的x值;
(3)当x为何值时,△NPC是一个等腰三角形?简要说明理由.
【答案】(1)P点坐标为(x,3﹣![]() x).
x).
(2)S的最大值为![]() ,此时x=2.
,此时x=2.
(3)x=![]() ,或x=
,或x=![]() ,或x=
,或x=![]() .
.
【解析】
试题分析:(1)求P点的坐标,也就是求OM和PM的长,已知了OM的长为x,关键是求出PM的长,方法不唯一,①可通过PM∥OC得出的对应成比例线段来求;
②也可延长MP交BC于Q,先在直角三角形CPQ中根据CQ的长和∠ACB的正切值求出PQ的长,然后根据PM=AB﹣PQ来求出PM的长.得出OM和PM的长,即可求出P点的坐标.
(2)可按(1)②中的方法经求出PQ的长,而CN的长可根据CN=BC﹣BN来求得,因此根据三角形的面积计算公式即可得出S,x的函数关系式.
(3)本题要分类讨论:
①当CP=CN时,可在直角三角形CPQ中,用CQ的长即x和∠ABC的余弦值求出CP的表达式,然后联立CN的表达式即可求出x的值;
②当CP=PN时,那么CQ=QN,先在直角三角形CPQ中求出CQ的长,然后根据QN=CN﹣CQ求出QN的表达式,根据题设的等量条件即可得出x的值.
③当CN=PN时,先求出QP和QN的长,然后在直角三角形PNQ中,用勾股定理求出PN的长,联立CN的表达式即可求出x的值.
试题解析:(1)过点P作PQ⊥BC于点Q,
有题意可得:PQ∥AB,
∴△CQP∽△CBA,
∴![]()
∴![]()
解得:QP=![]() x,
x,
∴PM=3﹣![]() x,
x,
由题意可知,C(0,3),M(x,0),N(4﹣x,3),
P点坐标为(x,3﹣![]() x).
x).
(2)设△NPC的面积为S,在△NPC中,NC=4﹣x,
NC边上的高为![]() ,其中,0≤x≤4.
,其中,0≤x≤4.
∴S=![]() (4﹣x)×
(4﹣x)×![]() x=
x=![]() (﹣x2+4x)
(﹣x2+4x)
=﹣![]() (x﹣2)2+
(x﹣2)2+![]() .
.
∴S的最大值为![]() ,此时x=2.
,此时x=2.
(3)延长MP交CB于Q,则有PQ⊥BC.
①若NP=CP,
∵PQ⊥BC,
∴NQ=CQ=x.
∴3x=4,
∴x=![]() .
.
②若CP=CN,则CN=4﹣x,PQ=x,CP=![]() x,4﹣x=
x,4﹣x=![]() x,
x,
∴x=![]() ;
;
③若CN=NP,则CN=4﹣x.
∵PQ=![]() x,NQ=4﹣2x,
x,NQ=4﹣2x,
∵在Rt△PNQ中,PN2=NQ2+PQ2,
∴(4﹣x)2=(4﹣2x)2+(![]() x)2,
x)2,
∴x=![]() .
.
综上所述,x=![]() ,或x=
,或x=![]() ,或x=
,或x=![]() .
.



 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:
【题目】(10分)如图,在Rt△ABC中,∠ACB=90°,D为AB的中点,且AE∥CD,CE∥AB.
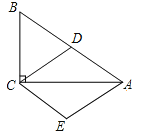
(1)四边形ADCE是菱形;
(2)若∠B=60°,BC=6,求菱形ADCE的高.(计算结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,M是边AB的中点,CH⊥AB于点H,CD平分∠ACB.

(1)求证:∠1=∠2.
(2)过点M作AB的垂线交CD的延长线于点E,连结AE,BE.求证:CM=EM.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有理数a,b,c在数轴上对应的点如图所示,则下列式子中正确的是( ) ![]()
A.a>b
B.|a﹣c|=a﹣c
C.﹣a<﹣b<c
D.|b+c|=b+c
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体育老师对甲、乙两名同学分别进行了8次跳高测试,经计算这两名同学成绩的平均数相同,甲同学的方差是S甲2=6.4,乙同学的方差是S乙2=8.2,那么这两名同学跳高成绩比较稳定的是同学.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下四个命题:
①若一个角的两边和另一个角的两边分别互相垂直,则这两个角互补;
②边数相等的两个正多边形一定相似;
③等腰三角形ABC中,D是底边BC上一点,E是一腰AC上的一点,若∠BAD=60°且AD=AE,则∠EDC=30°;
④任意三角形的外接圆的圆心一定是三角形三条边的垂直平分线的交点.
其中正确命题的序号为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把△ABC纸片沿DE折叠,当点A在四边形BCDE的外部时,记∠AEB为∠1,∠ADC为∠2,则∠A、∠1与∠2的数量关系,结论正确的是( )

A. ∠1=∠2+∠A B. ∠1=2∠A+∠2
C. ∠1=2∠2+2∠A D. 2∠1=∠2+∠A
查看答案和解析>>
科目:初中数学 来源: 题型:
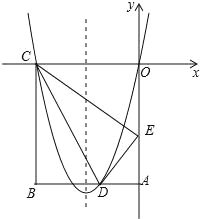
【题目】如图,在矩形OABC中,OA=5,AB=4,点D为边AB上一点,将△BCD沿直线CD折叠,使点B恰好落在边OA上的点E处,分别以OC,OA所在的直线为x轴,y轴建立平面直角坐标系.
(1)求OE的长及经过O,D,C三点抛物线的解析式;
(2)一动点P从点C出发,沿CB以每秒2个单位长度的速度向点B运动,同时动点Q从E点出发,沿EC以每秒1个单位长度的速度向点C运动,当点P到达点B时,两点同时停止运动,设运动时间为t秒,当t为何值时,DP=DQ;
(3)若点N在(1)中抛物线的对称轴上,点M在抛物线上,是否存在这样的点M与点N,使M,N,C,E为顶点的四边形是平行四边形?若存在,请求出M点坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com