
【题目】向阳村2017年的人均收入为30000元,2019年的人均收入为36300元.
(1)求2017年2019年该村人均收入的年平均增长率;
(2)假设2020年该村人均收入的增长率与前两年的年平均增长率相同,请你预测2020年该村的人均收入是多少元?
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
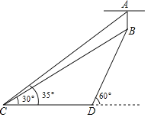
【题目】如图,宾馆大厅的天花板上挂有一盏吊灯AB,某人从C点测得吊灯顶端A的仰角为![]() ,吊灯底端B的仰角为
,吊灯底端B的仰角为![]() ,从C点沿水平方向前进6米到达点D,测得吊灯底端B的仰角为
,从C点沿水平方向前进6米到达点D,测得吊灯底端B的仰角为![]() .请根据以上数据求出吊灯AB的长度.(结果精确到0.1米.参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70,
.请根据以上数据求出吊灯AB的长度.(结果精确到0.1米.参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70,![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点
的图象交于点![]() ,与
,与![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,
,![]() 轴于点
轴于点![]() ,且
,且![]() .
.
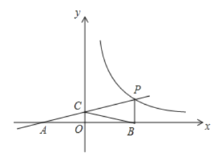
(1)求一次函数、反比例函数的解析式;
(2)根据图像直接写出![]() 的
的![]() 的取值范围;
的取值范围;
(3)点![]() 为反比例函数图象上使得四边形
为反比例函数图象上使得四边形![]() 为菱形的一点,点
为菱形的一点,点![]() 为
为![]() 轴上的一动点,当
轴上的一动点,当![]() 最大时,求点
最大时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“今天你光盘了吗?”这是国家倡导“厉行节约,反对浪费”以来的时尚流行语.某校团委随机抽取了部分学生,对他们进行了关于“光盘行动”所持态度的调查,并根据调查收集的数据绘制了如下两幅不完整的统计图:
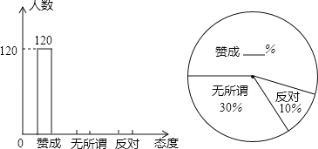
根据上述信息,解答下列问题:
(1)抽取的学生人数为 ;
(2)将两幅统计图补充完整;
(3)请你估计该校1200名学生中对“光盘行动”持赞成态度的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
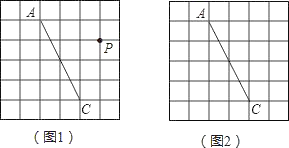
【题目】图1、图2是两张形状和大小完全相同的方格纸,方格纸中每个小正方形的边长均为1,线段AC的两个端点均在小正方形的顶点上.
(1)如图1,点P在小正方形的顶点上,在图1中作出点P关于直线AC的对称点Q,连接AQ、QC、CP、PA,并直接写出四边形AQCP的周长;
(2)在图2中画出一个以线段AC为对角线、面积为6的矩形ABCD,且点B和点D均在小正方形的顶点上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:把函数![]() 的图像绕点
的图像绕点![]() 旋转180°,得到新函数
旋转180°,得到新函数![]() 的图像,我们称
的图像,我们称![]() 是
是![]() 关于点
关于点![]() 的相关函数.
的相关函数.![]() 的图像的对称轴为直线
的图像的对称轴为直线![]() .例如:当
.例如:当![]() 时,函数
时,函数![]() 关于点
关于点![]() 的相关函数为
的相关函数为![]() .
.
(1)填空:![]() 的值为________(用含
的值为________(用含![]() 的代数式表示);
的代数式表示);
(2)若![]() ,
,![]() ,当
,当![]() 时,函数
时,函数![]() 的最大值为
的最大值为![]() ,最小值为
,最小值为![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
(3)当![]() 时,
时,![]() 的图像与
的图像与![]() 轴相交于
轴相交于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的右侧),与
的右侧),与![]() 轴相交于点
轴相交于点![]() .把线段
.把线段![]() 绕原点
绕原点![]() 顺时针旋转90°,得到它的对应线段
顺时针旋转90°,得到它的对应线段![]() .若线段
.若线段![]() 与
与![]() 的图像有公共点,结合函数图像,求
的图像有公共点,结合函数图像,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
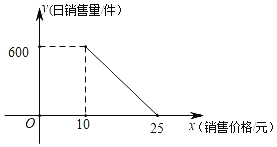
【题目】奏响复工复产“协奏曲”,防疫复产两不误.2020年2月5日,四川省出台《关于应对新型冠状病毒肺炎疫情缓解中小企业生产经营困难的政策措施》,推出减负降成本、破解融资难、财政补贴和税收减免、稳岗支持等13条举措,携手中小企业共渡难关.某企业积极复工复产,生产某种产品成本为9元/件,经过市场调查获悉,日销售量y(件)与销售价格x(元/件)的函数关系如图所示:
(1)求出y与x之间的函数表达式;
(2)当销售价格为多少元时,该企业日销售额为6000元?
(3)若该企业每销售1件产品可以获得2元财政补贴,则当销售价格x为何值时,该企业可以获最大日利润,最大日利润值为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
上课时孙老师提出这样一个问题:对于任意实数![]() ,关于
,关于![]() 的不等式
的不等式![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
小明的思路是:原不等式等价于![]() ,设函数
,设函数![]() ,
,![]() ,画出两个函数的图象的示意图,于是原问题转化为函数
,画出两个函数的图象的示意图,于是原问题转化为函数![]() 的图象在
的图象在![]() 的图象上方时
的图象上方时![]() 的取值范围.
的取值范围.

请结合小明的思路回答:
对于任意实数![]() ,关于
,关于![]() 的不等式
的不等式![]() 恒成立,则
恒成立,则![]() 的取值范围是_____.
的取值范围是_____.
参考小明思考问题的方法,解决问题:
关于![]() 的方程
的方程![]() 在
在![]() 范围内有两个解,求
范围内有两个解,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 是反比例函数
是反比例函数![]() 图象上的两点,
图象上的两点,![]() 轴,交
轴,交![]() 轴于点
轴于点![]() .动点
.动点![]() 从坐标原点
从坐标原点![]() 出发,沿
出发,沿![]() 匀速运动,终点为
匀速运动,终点为![]() .过点
.过点![]() 作
作![]() 轴于
轴于![]() .设
.设![]() 的面积为
的面积为![]() 点
点![]() 运动的时间为
运动的时间为![]() 则
则![]() 关于
关于![]() 的函数图象大致为( )
的函数图象大致为( )

A.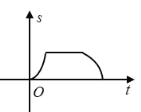 B.
B.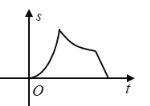
C. D.
D.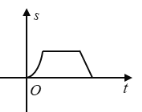
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com