练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    12．计算$\frac{1}{2}$cos30°的值为（　　）
    A．$\frac{1}{4}$B．$\frac{\sqrt{3}}{4}$C．1D．3

    分析 根据特殊角三角函数值，可得答案．

    解答 解：原式=$\frac{1}{2}$×$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{4}$，
    故选：B．

    点评 本题考查了特殊角三角函数值，熟记特殊角三角函数值是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    3．实数a、b在数轴上的位置如图所示，则化简   $\sqrt{{{（-a）}^2}}+\sqrt{b^2}-\sqrt{{{（a+b）}^2}}$的结果为2b．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

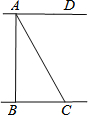    3．如图，河岸AD、BC互相平行，桥AB垂直于两岸，从C处看桥的两端A、B，夹角∠BCA=50度，测得BC=45m，则桥长AB=（　　）m．
    A．$\frac{45}{cos50°}$B．45•cos50°C．$\frac{45}{tan50°}$D．45•tan50°

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    20．如图，在直角坐标系中，已知点A（-3，0）、B（0，4），对△OAB连续作旋转变换，依次得到△1、△2、△3、△4…，则△2016的直角顶点的横坐标为（　　）
    A．8065B．8064C．8063D．8062

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

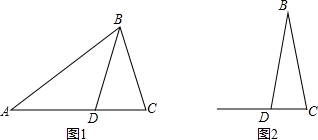    7．小明在做数学练习时，遇到下面的题目：
    题目：如图1，在△ABC中，D为AC边上一点，AB=AC，∠DBA=∠A，BD=BC．若CD=2，△BDC的周长为14，求AB的长．
    参考答案：AB=8．
    小明的计算结果与参考答案不同，因此他对参考答案产生了质疑．下面是他的分析、探究过程，请你补充完整．
    第一步，读题，并标记题目条件如下：
    在△ABC中，D为AC边上一点，①AB=AC；②∠DBA=∠A；③BD=BC；④CD=2；
    ⑤△BDC的周长为14．
    第二步，依据条件③、④、⑤，可以求得BD=BC=6；
    第三步，作出△BCD，如图2所示；
    第四步，依据条件①，在图2中作出△ABC；（尺规作图，保留作图痕迹）
    第五步，对所作图形进行观察、测量，发现与标记的条件②不符（填序号），去掉这个条件，题目中其他部分保持不变，求得AB的长为18．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    17．甲、乙两台机床同时生成一种零件，在5天中，两台机床每天生产出的次品数如表所列．
    甲02301
    乙12102
    分析上述数据，请你估计这两台机床的性能乙比较稳定（填“甲”或“乙”或“无法确定”）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

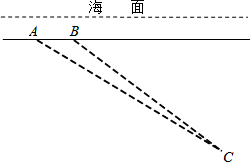    4．如图，一艘潜艇在海面下500m深的点A处，测得正前方俯角为31°方向上的海底有黑匣子发出信号，潜艇在同一深度保持直线航行500m，在点B处测得海底黑匣子位于正前方俯角36.9°的方向上，海底黑匣子C所在点距海面的深度为2000m．（精确到1，m．参考数据：sin36.9°≈0.60，cos36.9°≈0.80，tan36.9°≈0.75，sin31°≈0.51，cos31°≈0.87，tan31°≈0.60）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    1．下列命题中，不正确的是（　　）
    A．n边形的内角和等于（n-2）•180°
    B．边长分别为3，4，5，的三角形是直角三角形
    C．垂直于弦的直径平分弦所对的两条弧
    D．圆的切线垂直于半径

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    2．如图a是长方形纸带，∠DEF=21°，将纸带沿EF折叠成图b，再沿BF折叠成图c，则图c中的∠CFE的度数是（　　）
    A．117°B．119°C．138°D．159°

    查看答案和解析>>

    同步练习册答案