
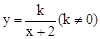 ��ͼ�����ɷ���������
��ͼ�����ɷ���������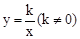 ��ͼ������ƽ��2����λ���ȵõ������������һ֪ʶ������⣮
��ͼ������ƽ��2����λ���ȵõ������������һ֪ʶ������⣮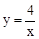 ��ͼ��C������������y=ax��a��0����ͼ��l�ཻ�ڵ�A��2��2���͵�B��
��ͼ��C������������y=ax��a��0����ͼ��l�ཻ�ڵ�A��2��2���͵�B��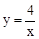 ��ͼ���ֱ��ABͬʱ����ƽ��n��n��0������λ���ȣ��õ���ͼ��ֱ��ΪC���l�䣬��֪ͼ��C�侭����M��2��4����
��ͼ���ֱ��ABͬʱ����ƽ��n��n��0������λ���ȣ��õ���ͼ��ֱ��ΪC���l�䣬��֪ͼ��C�侭����M��2��4����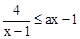 �Ľ⼯��
�Ľ⼯��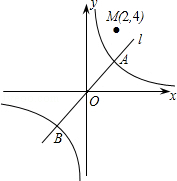
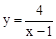 �� y=x��1��
�� y=x��1��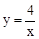 ��ͼ������ƽ��n��n��0������λ���ȣ��õ���ͼ��C��Ľ���ʽΪ
��ͼ������ƽ��n��n��0������λ���ȣ��õ���ͼ��C��Ľ���ʽΪ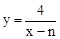 ��Ȼ���M��������뼴�ɵõ�n��ֵ��
��Ȼ���M��������뼴�ɵõ�n��ֵ��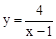 ��ͼ��l��Ľ���ʽΪy=x��1��
��ͼ��l��Ľ���ʽΪy=x��1��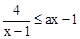 ������Ϊ�Ƚ�
������Ϊ�Ƚ�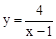 ��y=x��1�ĺ���ֵ������
��y=x��1�ĺ���ֵ������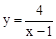 ��y=x��1Ϊ����
��y=x��1Ϊ����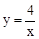 ��ͼ���ֱ��ABͬʱ����ƽ��1����λ���ȣ��õ���ͼ������������
��ͼ���ֱ��ABͬʱ����ƽ��1����λ���ȣ��õ���ͼ������������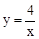 ��ͼ��������������y=ax��a��0����ͼ��Ľ���ΪA��2��2����B����2����2��������ƽ�ƺ�ֱ�Ϊ��3��2����B����1����2������x����1��0��x��2ʱ������
��ͼ��������������y=ax��a��0����ͼ��Ľ���ΪA��2��2����B����2����2��������ƽ�ƺ�ֱ�Ϊ��3��2����B����1����2������x����1��0��x��2ʱ������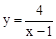 ��ͼ����y=x��1�ĺ���ͼ���Ϸ�����
��ͼ����y=x��1�ĺ���ͼ���Ϸ�����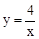 ��ͼ��������������y=x��ͼ��Ľ������ԭ��Գƣ�A��2��2����
��ͼ��������������y=x��ͼ��Ľ������ԭ��Գƣ�A��2��2����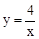 ��ͼ������ƽ��n��n��0������λ���ȣ��õ���ͼ��C��Ľ���ʽΪ
��ͼ������ƽ��n��n��0������λ���ȣ��õ���ͼ��C��Ľ���ʽΪ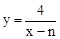 ��
��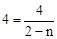 �����n=1��
�����n=1��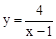 ��ͼ��l��Ľ���ʽΪy=x��1��
��ͼ��l��Ľ���ʽΪy=x��1��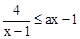 �Ľ⼯��x��3��1��x��1��
�Ľ⼯��x��3��1��x��1��

 ������ҵ����ν�����������ϵ�д�
������ҵ����ν�����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ ���ͣ������
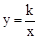 ��x��0����ͼ����B������B��BC��x���ڵ�C����P�Ǹ÷���������ͼ��������һ�㣬����P��PD��x���ڵ�D����Q���߶�AB������һ�㣬����OQ��CQ��
��x��0����ͼ����B������B��BC��x���ڵ�C����P�Ǹ÷���������ͼ��������һ�㣬����P��PD��x���ڵ�D����Q���߶�AB������һ�㣬����OQ��CQ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
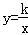 ��ͼ���ڵ�һ�����ڵĽ���ΪM��3��m����
��ͼ���ڵ�һ�����ڵĽ���ΪM��3��m����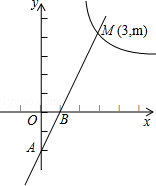
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
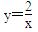 ��ͼ���ϵ����㣮AC��BD ����ֱ��x�ᣬ����ֱ�ΪC��D��AB���ӳ��߽�x���ڵ�E����C��D������ֱ�Ϊ(1��0)��(4��0)����BDE����� �릤ACE������ı�ֵ��__________��
��ͼ���ϵ����㣮AC��BD ����ֱ��x�ᣬ����ֱ�ΪC��D��AB���ӳ��߽�x���ڵ�E����C��D������ֱ�Ϊ(1��0)��(4��0)����BDE����� �릤ACE������ı�ֵ��__________�� 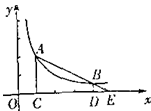
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
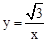 �ڵ�һ�����ڵ�ͼ��OB�ߵ��е�C�����B��������
�ڵ�һ�����ڵ�ͼ��OB�ߵ��е�C�����B��������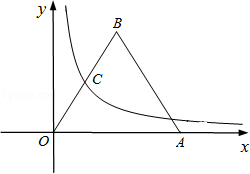
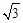 �� B����
�� B����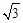 ��1�� C����2��
��1�� C����2��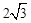 �� D����
�� D����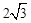 ��2��
��2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
 ��
��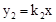 ��ͼ���ཻ�ڵ�A��1,2���͵�B����
��ͼ���ཻ�ڵ�A��1,2���͵�B����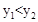 ʱ���Ա���x��ȡֵ��Χ�ǡ� ��
ʱ���Ա���x��ȡֵ��Χ�ǡ� ��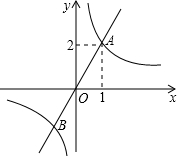
| A��x��1 | B����1��x��0 |
| C����1��x��0��x��1 | D��x����1��0��x��1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
 �У��Ա���x��ȡֵ��Χ�ǣ�������
�У��Ա���x��ȡֵ��Χ�ǣ�������| A��x��0 | B��x��0 | C��x��1 | D��x��1 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com