
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖĻ߶Ī![]() £¬
£¬ ![]() ŹĒ
ŹĒ![]() ÉĻµÄŅ»¶Æµć£¬
ÉĻµÄŅ»¶Æµć£¬![]() ŹĒ
ŹĒ![]() µÄÖŠµć£¬ŅŌ
µÄÖŠµć£¬ŅŌ![]() ĪŖ±ß×÷Õż·½ŠĪ
ĪŖ±ß×÷Õż·½ŠĪ![]() £¬µć
£¬µć![]() ¹ŲÓŚÉäĻß
¹ŲÓŚÉäĻß![]() µÄ¶Ō³ĘµćĪŖ
µÄ¶Ō³ĘµćĪŖ![]() £¬Į¬½Ó
£¬Į¬½Ó![]() ”¢
”¢![]() £¬Ö±Ļß
£¬Ö±Ļß![]() ½»
½»![]() ÓŚµć
ÓŚµć![]() £®
£®
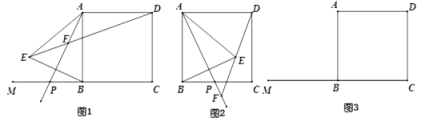
£Ø1£©ČēĶ¼1£¬µ±µć![]() ŌŚĻ߶Ī
ŌŚĻ߶Ī![]() ÉĻ£¬ĒŅ
ÉĻ£¬ĒŅ![]() £¬Ēó
£¬Ēó![]() µÄ¶ČŹż£»
µÄ¶ČŹż£»
£Ø2£©Š”Ć÷ŌŚ½āĢāŹ±·¢ĻÖ£ŗµ±µć![]() ŌŚĻ߶Ī
ŌŚĻ߶Ī![]() ÉĻŹ±£¬Ļ߶Ī
ÉĻŹ±£¬Ļ߶Ī![]() £¬
£¬![]() £¬
£¬![]() Ö®¼äĀś×ć
Ö®¼äĀś×ć![]() £¬ÄĒĆ“ÄćČĻĪŖµ±µć
£¬ÄĒĆ“ÄćČĻĪŖµ±µć![]() ŌŚĻ߶Ī
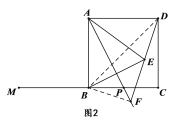
ŌŚĻ߶Ī![]() ÉĻŹ±£ØČēĶ¼2£©£¬ĖūµÄ½įĀŪŹĒ·ń»¹³ÉĮ¢£æČō³ÉĮ¢£¬ĒėÖ¤Ć÷£¬Čō²»³ÉĮ¢£¬ĒėĖµĆ÷ĄķÓÉ£»
ÉĻŹ±£ØČēĶ¼2£©£¬ĖūµÄ½įĀŪŹĒ·ń»¹³ÉĮ¢£æČō³ÉĮ¢£¬ĒėÖ¤Ć÷£¬Čō²»³ÉĮ¢£¬ĒėĖµĆ÷ĄķÓÉ£»
£Ø3£©ČēĶ¼3£¬µć![]() ŌŚ
ŌŚ![]() ÉĻ£¬ĒŅ
ÉĻ£¬ĒŅ![]() £¬µ±µć
£¬µ±µć![]() “Óµć
“Óµć![]() ŌĖ¶Æµ½µć
ŌĖ¶Æµ½µć![]() Ź±£¬Ö±½ÓŠ“³öµć
Ź±£¬Ö±½ÓŠ“³öµć![]() Ėł¾¹żµÄĀ·¾¶³¤£®
Ėł¾¹żµÄĀ·¾¶³¤£®
”¾“š°ø”æ£Ø1£©”ĻAFD=45 £»£Ø2£©³ÉĮ¢£¬ĄķÓɼū½āĪö£»£Ø3£©µć![]() Ėł¾¹żµÄĀ·¾¶³¤ĪŖ
Ėł¾¹żµÄĀ·¾¶³¤ĪŖ![]() £®
£®
”¾½āĪö”æ
£Ø1£©øł¾Żµć![]() ¹ŲÓŚÉäĻß
¹ŲÓŚÉäĻß![]() µÄ¶Ō³ĘµćĪŖ
µÄ¶Ō³ĘµćĪŖ![]() £¬µĆ³öAE=AB£¬”ĻEAP=”ĻPAB=25£¬ŌŁøł¾ŻÕż·½ŠĪŗĶµČŃüČż½ĒŠĪµÄŠŌÖŹµĆ³ö”ĻAED£¬Č»ŗóøł¾ŻČż½ĒŠĪµÄĶā½Ē¼“æÉµĆ³ö½įĀŪ
£¬µĆ³öAE=AB£¬”ĻEAP=”ĻPAB=25£¬ŌŁøł¾ŻÕż·½ŠĪŗĶµČŃüČż½ĒŠĪµÄŠŌÖŹµĆ³ö”ĻAED£¬Č»ŗóøł¾ŻČż½ĒŠĪµÄĶā½Ē¼“æÉµĆ³ö½įĀŪ
£Ø2£©Į¬½ÓBF”¢BD£¬ĻČøł¾ŻÕż·½ŠĪµÄŠŌÖŹæɵĆBD=2AD£¬ŌŁøł¾ŻČż½ĒŠĪµÄĶā½ĒŗĶÄŚ½ĒŗĶ¶ØĄķµĆ³ö”ĻAFD=45£¬“ÓČ·¶ØBFD ŹĒÖ±½ĒČż½ĒŠĪ£¬¼“æÉµĆ³ö½įĀŪ
£Ø3£©µ±µćPŌĖ¶Æµ½µćQŹ±£¬BP=2£¬½āÖ±½ĒČż½ĒŠĪ”÷ABP£¬µĆ³ö”ĻBAP=30£¬ŌŁøł¾Ż”ĻAFD=![]() ”ĻAOD£¬æɵƵćFĖł¾¹żµÄĀ·¾¶³¤ĪŖŅŌµćOĪŖŌ²ŠÄ£¬ŅŌOA³¤ĪŖ°ė¾¶£¬Ō²ŠÄ½Ē”ĻAOF=150µÄ»”³¤£¬¼“æÉĒó³ö“š°ø
”ĻAOD£¬æɵƵćFĖł¾¹żµÄĀ·¾¶³¤ĪŖŅŌµćOĪŖŌ²ŠÄ£¬ŅŌOA³¤ĪŖ°ė¾¶£¬Ō²ŠÄ½Ē”ĻAOF=150µÄ»”³¤£¬¼“æÉĒó³ö“š°ø
£Ø1£©Ö¤Ć÷£ŗ”ßĖıߊĪABCDŹĒÕż·½ŠĪ
”ąAB=AD£¬”ĻBAD=90
”ßµćBÓėµćE¹ŲÓŚÉäĻßAP¶Ō³Ę
”ąAE=AB£¬”ĻEAP=”ĻPAB=25
”ąAE=AD£¬”ĻEAD=”ĻEAB+”ĻBAD=140
”ą”ĻAED=![]() (180-”ĻEAD)=
(180-”ĻEAD)= ![]() (180-140)=20
(180-140)=20
”ą”ĻAFD=”ĻAED+”ĻEAP=20+25=45
£Ø2£©³ÉĮ¢
ĄķÓÉČēĻĀ£ŗĮ¬½ÓBF”¢BD£¬
ŌŚRtABDÖŠ£¬BD=AB+AD=2AD
”ßµćBÓėµćE¹ŲÓŚÉäĻßAP¶Ō³Ę
”ąBF=EF £¬AB=AE=AD£¬”ĻAFB=”ĻAFD
”ą”ĻBAF=”ĻEAF£¬”ĻADE=”ĻAED
”ß”ĻAEDŹĒ”÷AEFµÄĶā½Ē
”ą”ĻAED=”ĻEAF+”ĻAFD
Ó֔ߔĻDAE=90£2”ĻEAF
”ąŌŚ”÷ADEÖŠ£¬”ĻDAE+”ĻADE+”ĻAED=180
”ą90£2”ĻEAF+2(”ĻEAF+”ĻAFD)=180
”ą”ĻAFD=45
”ą”ĻBFD=2”ĻAFD=90
”ąŌŚRtBFDÖŠ£¬B F+DF=BD
”ąEF+DF=2AD
£Ø3£©µć![]() Ėł¾¹żµÄĀ·¾¶³¤ĪŖ
Ėł¾¹żµÄĀ·¾¶³¤ĪŖ![]() £®
£®

ÉčAC”¢BDĻą½»ÓŚµćO£¬Ōņ
OA=![]() AB=
AB=![]()
”ßŌŚµćFµÄŌĖ¶Æ¹ż³ĢÖŠ£¬”ĻAFD=45
”ą”ĻAFD=![]() ”ĻAOD
”ĻAOD
µ±µćPŌĖ¶Æµ½µćQŹ±£¬BP=2
ŌŚRt”÷ABPÖŠ£¬tan”ĻBAP=![]()
”ą”ĻBAP=30”ą”ĻCAF=15
”ąµćFĖł¾¹żµÄĀ·¾¶³¤ĪŖŅŌµćOĪŖŌ²ŠÄ£¬ŅŌOA
”ąµćFĖł¾¹żµÄĀ·¾¶³¤ĪŖ![]() £®
£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ³É¶¼ŹŠÄ³ĘóŅµ»ż¼«ĻģÓ¦Õžø®”°““ŠĀ·¢Õ¹”±µÄŗÅÕŁ£¬ŃŠ·¢ĮĖŅ»ÖÖŠĀ²śĘ·£®ŅŃÖŖŃŠ·¢”¢Éś²śÕāÖÖŠĀ²śĘ·µÄ³É±¾ĪŖ30ŌŖ/¼ž£¬¾ŹŠ³”µ÷²é·¢ĻÖ£¬øĆ²śĘ·µÄÄźĻśŹŪĮæy£ØĶņ¼ž£©ÓėĻśŹŪµ„¼Ūx£ØŌŖ£©Ö®¼äµÄŗÆŹż¹ŲĻµČēĻĀĶ¼£ŗ
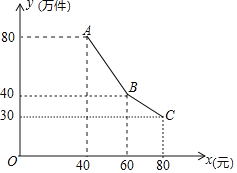
£Ø1£©Ēó³öyÓėxÖ®¼äµÄŗÆŹż¹ŲĻµŹ½£»
£Ø2£©µ±øĆ²śĘ·µÄŹŪ¼ŪĪŖ¶ąÉŁŹ±£¬øĆĘóŅµĻśŹŪøĆ²śĘ·»ńµĆµÄÄźĄūČó×ī“ó£æ×ī“óÄźĄūČóŹĒ¶ąÉŁ£æ£Ø×¢£ŗÄźĄūČó£½ÄźĻśŹŪĮæ”Į£ØĻśŹŪµ„¼Ū©³É±¾µ„¼Ū£©£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
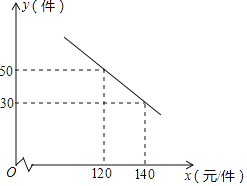
”¾ĢāÄæ”æijÉĢ³”¹ŗ½ųŅ»ÖÖĆ漞¼ŪøńĪŖ90ŌŖµÄŠĀÉĢĘ·£¬ŌŚÉĢ³”ŹŌĻśŹ±·¢ĻÖ£ŗĻśŹŪµ„¼Ū![]() ŌŖ
ŌŖ![]() ¼ž
¼ž![]() ÓėĆæĢģĻśŹŪĮæ
ÓėĆæĢģĻśŹŪĮæ![]() ¼ž
¼ž![]() Ö®¼äĀś×ćČēĶ¼ĖłŹ¾µÄ¹ŲĻµ£®
Ö®¼äĀś×ćČēĶ¼ĖłŹ¾µÄ¹ŲĻµ£®
![]() Ēó³öyÓėxÖ®¼äµÄŗÆŹż¹ŲĻµŹ½£»
Ēó³öyÓėxÖ®¼äµÄŗÆŹż¹ŲĻµŹ½£»
![]() Š“³öĆæĢģµÄĄūČóWÓėĻśŹŪµ„¼ŪxÖ®¼äµÄŗÆŹż¹ŲĻµŹ½£¬²¢Ēó³öŹŪ¼Ū¶ØĪŖ¶ąÉŁŹ±£¬ĆæĢģ»ńµĆµÄĄūČó×ī“ó£æ×ī“óĄūČóŹĒ¶ąÉŁ£æ
Š“³öĆæĢģµÄĄūČóWÓėĻśŹŪµ„¼ŪxÖ®¼äµÄŗÆŹż¹ŲĻµŹ½£¬²¢Ēó³öŹŪ¼Ū¶ØĪŖ¶ąÉŁŹ±£¬ĆæĢģ»ńµĆµÄĄūČó×ī“ó£æ×ī“óĄūČóŹĒ¶ąÉŁ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
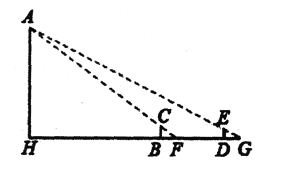
”¾ĢāÄæ”收ŗ£µŗĖć¾”·µŚŅ»øöĪŹĢāµÄ“óŅāŹĒ£ŗČēĶ¼£¬ŅŖ²āĮæŗ£µŗÉĻŅ»×łÉ½·å![]() µÄø߶Č
µÄø߶Č![]() £¬Į¢Į½øłøß
£¬Į¢Į½øłøß![]() ÕɵıźøĖ
ÕɵıźøĖ![]() ŗĶ
ŗĶ![]() £¬Į½øĶÖ®¼äµÄ¾ą
£¬Į½øĶÖ®¼äµÄ¾ą![]() ²½£¬
²½£¬![]() ³ÉŅ»Ļߣ¬“Ó
³ÉŅ»Ļߣ¬“Ó![]() “¦ĶĖŠŠ
“¦ĶĖŠŠ![]() ²½µ½
²½µ½![]() £¬ČĖµÄŃŪ¾¦Ģł×ŵŲĆę¹Ū²ģ
£¬ČĖµÄŃŪ¾¦Ģł×ŵŲĆę¹Ū²ģ![]() µć£¬
µć£¬![]() Čżµć³ÉŅ»Ļߣ»“Ó
Čżµć³ÉŅ»Ļߣ»“Ó![]() “¦ĶĖŠŠ
“¦ĶĖŠŠ![]() ²½µ½
²½µ½![]() £¬“Ó
£¬“Ó![]() ¹Ū²ģ
¹Ū²ģ![]() µć£¬
µć£¬![]() ČżµćŅ²³ÉŅ»-Ļߣ®ŹŌ¼ĘĖćɽ·åµÄø߶Č
ČżµćŅ²³ÉŅ»-Ļߣ®ŹŌ¼ĘĖćɽ·åµÄø߶Č![]() ¼°
¼°![]() µÄ³¤£® (ÕāĄļ
µÄ³¤£® (ÕāĄļ![]() ²½
²½![]() ³ß£¬
³ß£¬![]() ÕÉ
ÕÉ![]() ³ß£¬½į¹ūÓĆÕɱķŹ¾) £®ŌõŃłĄūÓĆĻąĖĘČż½ĒŠĪĒóµĆĻ߶Ī
³ß£¬½į¹ūÓĆÕɱķŹ¾) £®ŌõŃłĄūÓĆĻąĖĘČż½ĒŠĪĒóµĆĻ߶Ī![]() ¼°
¼°![]() µÄ³¤ÄŲ£æĒėÄćŹŌŅ»ŹŌ!
µÄ³¤ÄŲ£æĒėÄćŹŌŅ»ŹŌ!
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
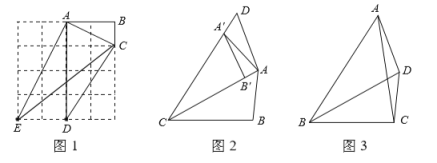
”¾ĢāÄæ”æ¶ØŅå£ŗČōŅ»øöĖıߊĪÄܱ»ĘäÖŠŅ»Ģõ¶Ō½ĒĻß·Öøī³ÉĮ½øöĻąĖĘČż½ĒŠĪ£¬Ōņ³ĘÕāøöĖıߊĪĪŖ”°ÓŃŗĆĖıߊĪ”±£®
£Ø1£©ČēĶ¼1£¬ŌŚ![]() µÄÕż·½ŠĪĶųøńÖŠ£¬ÓŠŅ»øöĶųøń
µÄÕż·½ŠĪĶųøńÖŠ£¬ÓŠŅ»øöĶųøń![]() ŗĶĮ½øöĶųøńĖıߊĪ
ŗĶĮ½øöĶųøńĖıߊĪ![]() Óė
Óė![]() £¬ĘäÖŠŹĒ±»
£¬ĘäÖŠŹĒ±»![]() ·Öøī³ÉµÄ”°ÓŃŗĆĖıߊĪ”±µÄŹĒ £»
·Öøī³ÉµÄ”°ÓŃŗĆĖıߊĪ”±µÄŹĒ £»
£Ø2£©ČēĶ¼2£¬½«![]() Čʵć
Čʵć![]() ÄꏱÕėŠż×ŖµĆµ½
ÄꏱÕėŠż×ŖµĆµ½![]() £¬µć
£¬µć![]() ĀäŌŚ±ß
ĀäŌŚ±ß![]() £¬¹żµć
£¬¹żµć![]() ×÷
×÷![]() ½»
½»![]() µÄŃÓ³¤ĻßÓŚµć
µÄŃÓ³¤ĻßÓŚµć![]() £¬ĒóÖ¤£ŗĖıߊĪ
£¬ĒóÖ¤£ŗĖıߊĪ![]() ŹĒ”°ÓŃŗĆĖıߊĪ”±£»
ŹĒ”°ÓŃŗĆĖıߊĪ”±£»
£Ø3£©ČēĶ¼3£¬ŌŚ![]() ÖŠ£¬
ÖŠ£¬![]() £¬
£¬![]() £¬
£¬![]() µÄĆ껿ĪŖ
µÄĆ껿ĪŖ![]() £¬µć
£¬µć![]() ŹĒ
ŹĒ![]() µÄĘ½·ÖĻßÉĻŅ»µć£¬Į¬½Ó
µÄĘ½·ÖĻßÉĻŅ»µć£¬Į¬½Ó![]() £¬
£¬![]() £®ČōĖıߊĪ
£®ČōĖıߊĪ![]() ŹĒ±»
ŹĒ±»![]() ·Öøī³ÉµÄ”°ÓŃŗĆĖıߊĪ”±£¬Ēó
·Öøī³ÉµÄ”°ÓŃŗĆĖıߊĪ”±£¬Ēó![]() µÄ³¤£®
µÄ³¤£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬µć![]() ŌŚĘ½ŠŠĖıߊĪ
ŌŚĘ½ŠŠĖıߊĪ![]() µÄ¶Ō½ĒĻß
µÄ¶Ō½ĒĻß![]() ÉĻ£¬¹żµć
ÉĻ£¬¹żµć![]() ”¢
”¢![]() ·Ö±š×÷
·Ö±š×÷![]() ”¢
”¢![]() µÄĘ½ŠŠĻßĻą½»ÓŚµć
µÄĘ½ŠŠĻßĻą½»ÓŚµć![]() £¬Į¬½Ó
£¬Į¬½Ó![]() £¬
£¬![]() £®
£®
£Ø1£©ĒóÖ¤£ŗĖıߊĪ![]() ŹĒĮāŠĪ£»
ŹĒĮāŠĪ£»
£Ø2£©Čō![]() £¬
£¬![]() £¬
£¬![]() £¬Ēó
£¬Ēó![]() µÄ³¤£®
µÄ³¤£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
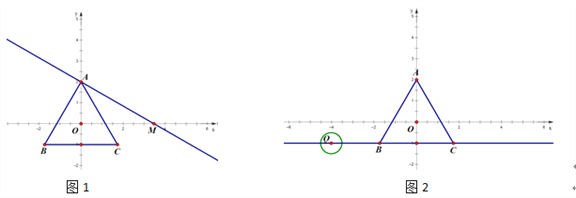
”¾ĢāÄæ”æÉčĘ½ĆęÄŚŅ»µćµ½µČ±ßČż½ĒŠĪÖŠŠÄµÄ¾ąĄėĪŖd£¬µČ±ßČż½ĒŠĪµÄÄŚĒŠŌ²°ė¾¶ĪŖr£¬Ķā½ÓŌ²°ė¾¶ĪŖR .¶ŌÓŚŅ»øöµćÓėµČ±ßČż½ĒŠĪ£¬øų³öČēĻĀ¶ØŅå£ŗĀś×ćr”Üd”ÜRµÄµć½Š×öµČ±ßČż½ĒŠĪµÄÖŠŠÄ¹ŲĮŖµć.ŌŚĘ½ĆęÖ±½Ē×ų±źĻµxOyÖŠ£¬µČ±ß”÷ABCµÄČżøö¶„µćµÄ×ų±ź·Ö±šĪŖA(0£¬2)£¬B£Ø©![]() £¬©1£©£¬C(
£¬©1£©£¬C(![]() £¬©1).
£¬©1).
£Ø1£©ŅŃÖŖµćD£Ø2£¬2£©£¬E£Ø![]() £¬1£©£¬F£Ø
£¬1£©£¬F£Ø![]() £¬©1£©.ŌŚD£¬E£¬FÖŠ£¬ŹĒµČ±ß”÷ABCµÄÖŠŠÄ¹ŲĮŖµćµÄŹĒ £»
£¬©1£©.ŌŚD£¬E£¬FÖŠ£¬ŹĒµČ±ß”÷ABCµÄÖŠŠÄ¹ŲĮŖµćµÄŹĒ £»
£Ø2£©ČēĶ¼1£¬¹żµćA×÷Ö±Ļß½»xÖįÕż°ėÖįÓŚM£¬Ź¹”ĻAMO=30”ć.
¢ŁČōĻ߶ĪAMÉĻ“ęŌŚµČ±ß”÷ABCµÄÖŠŠÄ¹ŲĮŖµćP£Øm£¬n£©£¬ĒómµÄȔֵ·¶Ī§£»
¢Ś½«Ö±ĻßAMĻņĻĀĘ½ŅʵƵ½Ö±Ļßy=kx+b£¬µ±bĀś×ćŹ²Ć“Ģõ¼žŹ±£¬Ö±Ļßy=kx+bÉĻ×Ü“ęŌŚµČ±ß”÷ABCµÄÖŠŠÄ¹ŲĮŖµć£»£ØÖ±½ÓŠ“³ö“š°ø£¬²»Šč¹ż³Ģ£©
£Ø3£©ČēĶ¼2£¬µćQĪŖÖ±Ļßy=©1ÉĻŅ»¶Æµć£¬”ŃQµÄ°ė¾¶ĪŖ![]() .µ±Q“Óµć£Ø©4£¬©1£©³ö·¢£¬ŅŌĆæĆė1øöµ„Ī»µÄĖŁ¶ČĻņÓŅŅĘ¶Æ£¬ŌĖ¶ÆŹ±¼äĪŖtĆė.ŹĒ·ń“ęŌŚÄ³Ņ»Ź±æĢt£¬Ź¹µĆ”ŃQÉĻĖłÓŠµć¶¼ŹĒµČ±ß”÷ABCµÄÖŠŠÄ¹ŲĮŖµć£æČē¹ū“ęŌŚ£¬ĒėÖ±½ÓŠ“³öĖłÓŠ·ūŗĻĢāŅāµÄtµÄÖµ£»Čē¹ū²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ.
.µ±Q“Óµć£Ø©4£¬©1£©³ö·¢£¬ŅŌĆæĆė1øöµ„Ī»µÄĖŁ¶ČĻņÓŅŅĘ¶Æ£¬ŌĖ¶ÆŹ±¼äĪŖtĆė.ŹĒ·ń“ęŌŚÄ³Ņ»Ź±æĢt£¬Ź¹µĆ”ŃQÉĻĖłÓŠµć¶¼ŹĒµČ±ß”÷ABCµÄÖŠŠÄ¹ŲĮŖµć£æČē¹ū“ęŌŚ£¬ĒėÖ±½ÓŠ“³öĖłÓŠ·ūŗĻĢāŅāµÄtµÄÖµ£»Čē¹ū²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijÓĪĄÖ³”ŹŌÓŖŅµĘŚ¼ä£¬ĆæĢģŌĖÓŖ³É±¾ĪŖ1000ŌŖ.¾Ķ³¼Ę·¢ĻÖ£¬ĆæĢģŹŪ³öµÄĆÅʱÕÅŹż![]() £ØÕÅ£©ÓėĆÅʱŹŪ¼Ū
£ØÕÅ£©ÓėĆÅʱŹŪ¼Ū![]() £ØŌŖ/ÕÅ£©Ö®¼äĀś×ćŅ»“ĪŗÆŹż
£ØŌŖ/ÕÅ£©Ö®¼äĀś×ćŅ»“ĪŗÆŹż![]() £¬ÉčÓĪĄÖ³”ĆæĢģµÄĄūČóĪŖ
£¬ÉčÓĪĄÖ³”ĆæĢģµÄĄūČóĪŖ![]() £ØŌŖ£©.£ØĄūČó=ʱ·æŹÕČė£ŌĖÓŖ³É±¾£©
£ØŌŖ£©.£ØĄūČó=ʱ·æŹÕČė£ŌĖÓŖ³É±¾£©
£Ø1£©ŹŌĒó![]() Óė
Óė![]() Ö®¼äµÄŗÆŹż±ķ“ļŹ½.
Ö®¼äµÄŗÆŹż±ķ“ļŹ½.
£Ø2£©ÓĪĄÖ³”½«ĆÅʱŹŪ¼Ū¶ØĪŖ¶ąÉŁŌŖ/ÕÅŹ±£¬ĆæĢģ»ńĄū×ī“ó£æ×ī“óĄūČóŹĒ¶ąÉŁŌŖ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
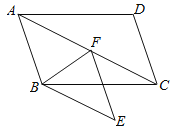
”¾ĢāÄæ”æŌŚ![]() ÖŠ£¬E,F·Ö±šŹĒAB,DCÉĻµÄµć£¬ĒŅ
ÖŠ£¬E,F·Ö±šŹĒAB,DCÉĻµÄµć£¬ĒŅ![]() £¬Į¬½ÓDE,BF,AF.
£¬Į¬½ÓDE,BF,AF.
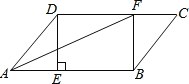
£Ø1£©ĒóÖ¤£ŗĖıߊĪDEBFŹĒĘ½ŠŠĖıߊĪ£»
£Ø2£©ČōAFĘ½·Ö![]() £¬ĒóAFµÄ³¤.
£¬ĒóAFµÄ³¤.
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com