
”¾ĢāÄæ”æČżøöŠ”ĒņÉĻ·Ö±š±źÓŠŹż×Ö©2£¬©1£¬3£¬ĖüĆĒ³żŹż×ÖĶāĘäӹȫ²æĻąĶ¬£¬ĻÖ½«ĖüĆĒ·ÅŌŚŅ»øö²»ĶøĆ÷µÄ“ü×ÓĄļ£¬“Ó“ü×ÓÖŠĖ껜µŲĆž³öŅ»Ēņ£¬½«ĒņÉĻµÄŹż×Ö¼ĒĀ¼£¬¼ĒĪŖm£¬Č»ŗó·Å»Ų£»ŌŁĖ껜µŲƞȔŅ»Ēņ£¬½«ĒņÉĻµÄŹż×Ö¼ĒĀ¼£¬¼ĒĪŖn£¬Õāѳȷ¶ØĮĖµć(m£¬n)£®
£Ø1£©ĒėĮŠ±ķ»ņ»³öŹ÷דĶ¼£¬²¢øł¾ŻĮŠ±ķ»ņŹ÷דĶ¼Š“³öµć(m£¬n)ĖłÓŠæÉÄܵĽį¹ū£»
£Ø2£©Ēóµć(m£¬n)ŌŚŗÆŹży£½xµÄĶ¼ĻóÉĻµÄøÅĀŹ£®
”¾“š°ø”æ£Ø1£©¼ū½āĪö£»£Ø2£©![]()
”¾½āĪö”æ
£Ø1£©øł¾ŻĢāŅāĮŠ±ķ£¬Č»ŗ󊓳öµć£Øm£¬n£©ĖłÓŠæÉÄܵĽį¹ū¼“æÉ£»
£Ø2£©µć£Øm£¬n£©ĖłÓŠæÉÄܵĽį¹ū¹²ÓŠ9ÖÖ£¬·ūŗĻn£½mµÄÓŠ3ÖÖ£¬ÓÉøÅĀŹ¹«Ź½¼“æÉµĆ³ö“š°ø£®
½ā£ŗ£Ø1£©ĮŠ±ķČēĻĀ£ŗ
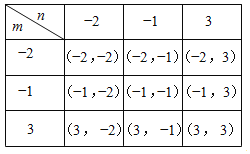
µć£Øm£¬n£©ĖłÓŠæÉÄܵĽį¹ūĪŖ£ŗ£Ø©2£¬©2£©£¬£Ø©1£¬©2£©£¬£Ø3£¬©2£©£¬£Ø©2£¬©1£©£¬£Ø©1£¬©1£©£¬£Ø3£¬©1£©£¬£Ø©2£¬3£©£¬£Ø©1£¬3£©£Ø3£¬3£©£»
£Ø2£©µć£Øm£¬n£©ĖłÓŠæÉÄܵĽį¹ū¹²ÓŠ9ÖÖ£¬·ūŗĻn£½mµÄÓŠ3ÖÖ£ŗ£Ø©2£¬©2£©£¬£Ø©1£¬©1£©£¬£Ø3£¬3£©£¬
”ąµć£Øm£¬n£©ŌŚŗÆŹży£½xµÄĶ¼ĻóÉĻµÄøÅĀŹĪŖ£ŗ![]() £®
£®


 ĢģĢģĻņÉĻŅ»±¾ŗĆ¾ķĻµĮŠ“š°ø
ĢģĢģĻņÉĻŅ»±¾ŗĆ¾ķĻµĮŠ“š°ø Š”ѧɜ10·ÖÖÓÓ¦ÓĆĢāĻµĮŠ“š°ø
Š”ѧɜ10·ÖÖÓÓ¦ÓĆĢāĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
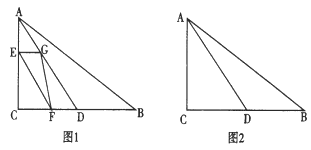
”¾ĢāÄæ”æČēĶ¼1£¬”÷ABCÖŠ£¬”ĻACB=90”ć£¬AC=4cm£¬BC=6cm£¬DŹĒBCµÄÖŠµć.µćE“ÓA³ö·¢£¬ŅŌacm/s(a£¾0)µÄĖŁ¶ČŃŲACŌČĖŁĻņµćCŌĖ¶Æ£»µćFĶ¬Ź±ŅŌ1cm/sµÄĖŁ¶Č“ÓµćC³ö·¢£¬ŃŲCBŌČĖŁĻņµćBŌĖ¶Æ£¬ĘäÖŠŅ»øö¶Æµćµ½“ļ¶ĖµćŹ±£¬ĮķŅ»øö¶ÆµćŅ²ĖęÖ®Ķ£Ö¹ŌĖ¶Æ£¬¹żµćE×÷ACµÄ“¹Ļߣ¬½»ADÓŚµćG£¬Į¬½ÓEF£¬FG£¬ÉčĖüĆĒŌĖ¶ÆµÄŹ±¼äĪŖtĆė(t”Żt0).
(1)Čōt=2£¬”÷CEF”×”÷ABC£¬ĒóaµÄÖµ£»
(2)µ±a=![]() Ź±£¬ŅŌµćE”¢F”¢D”¢GĪŖ¶„µćµćĖıߊĪŹ±Ę½ŠŠĖıߊĪ£¬ĒótµÄÖµ£»
Ź±£¬ŅŌµćE”¢F”¢D”¢GĪŖ¶„µćµćĖıߊĪŹ±Ę½ŠŠĖıߊĪ£¬ĒótµÄÖµ£»
(3)Čōa=2£¬ŹĒ·ń“ęŌŚŹµŹżt£¬Ź¹µĆµć”÷DFGŹĒÖ±½ĒČż½ĒŠĪ£æČō“ęŌŚ£¬ĒėĒó³ötµÄÖµ£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĀęĶÕ±»³ĘĪŖ”°É³Ä®Ö®ÖŪ”±£¬ĖüµÄĢåĪĀĖꏱ¼äµÄ±ä»Æ¶ų·¢Éś½Ļ“ó±ä»Æ£¬ĘäĢåĪĀ£Ø![]() £©ÓėŹ±¼ä£ØŠ”Ź±£©Ö®¼äµÄ¹ŲĻµČēĶ¼1ĖłŹ¾£®
£©ÓėŹ±¼ä£ØŠ”Ź±£©Ö®¼äµÄ¹ŲĻµČēĶ¼1ĖłŹ¾£®

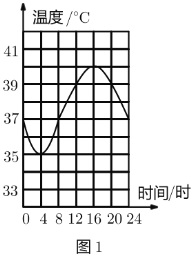
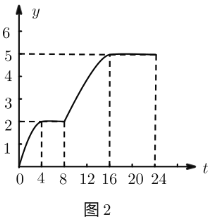
Š”ĒåĶ¬Ń§øł¾ŻĶ¼1»ęÖĘĮĖĶ¼2£¬ŌņĶ¼2ÖŠµÄ±äĮæÓŠæÉÄܱķŹ¾µÄŹĒ£Ø £©£®
A.ĀęĶÕŌŚ![]() Ź±æĢµÄĢåĪĀÓė0Ź±ĢåĪĀµÄ¾ų¶Ō²ī£Ø¼“²īµÄ¾ų¶ŌÖµ£©
Ź±æĢµÄĢåĪĀÓė0Ź±ĢåĪĀµÄ¾ų¶Ō²ī£Ø¼“²īµÄ¾ų¶ŌÖµ£©
B.ĀęĶÕ“Ó0Ź±µ½![]() Ź±æĢÖ®¼äµÄ×īøßĢåĪĀÓėµ±ČÕ×īµĶĢåĪĀµÄ²ī
Ź±æĢÖ®¼äµÄ×īøßĢåĪĀÓėµ±ČÕ×īµĶĢåĪĀµÄ²ī
C.ĀęĶÕŌŚ![]() Ź±æĢµÄĢåĪĀÓėµ±ČÕĘ½¾łĢåĪĀµÄ¾ų¶Ō²ī
Ź±æĢµÄĢåĪĀÓėµ±ČÕĘ½¾łĢåĪĀµÄ¾ų¶Ō²ī
D.ĀęĶÕ“Ó0Ź±µ½![]() Ź±æĢÖ®¼äµÄĢåĪĀ×ī“óÖµÓė×īŠ”ÖµµÄ²ī
Ź±æĢÖ®¼äµÄĢåĪĀ×ī“óÖµÓė×īŠ”ÖµµÄ²ī
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
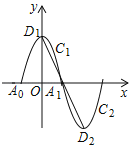
”¾ĢāÄæ”æČēĶ¼£¬Ņ»¶ĪÅ×ĪļĻßy£½©x2+4£Ø©2”Üx”Ü2£©ĪŖC1£¬ÓėxÖį½»ÓŚA0£¬A1Į½µć£¬¶„µćĪŖD1£»½«C1ČʵćA1Šż×Ŗ180”ćµĆµ½C2£¬¶„µćĪŖD2£»C1ÓėC2×é³ÉŅ»øöŠĀµÄĶ¼Ļ󣬓¹Ö±ÓŚyÖįµÄÖ±ĻßlÓėŠĀĶ¼Ļó½»ÓŚµćP1£Øx1£¬y1£©£¬P2£Øx2£¬y2£©£¬ÓėĻ߶ĪD1D2½»ÓŚµćP3£Øx3£¬y3£©£¬Éčx1£¬x2£¬x3¾łĪŖÕżŹż£¬t£½x1+x2+x3£¬ŌņtµÄȔֵ·¶Ī§ŹĒ_____£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ4”Į4µÄĶųøńÖŠ£¬µćA£¬B£¬C£¬D£¬H¾łŌŚĶųøńµÄøńµćÉĻ£¬ĻĀĆę½įĀŪ£ŗ
¢ŁµćHŹĒ”÷ABDµÄÄŚŠÄ
¢ŚµćHŹĒ”÷ABDµÄĶāŠÄ
¢ŪµćHŹĒ”÷BCDµÄĶāŠÄ
¢ÜµćHŹĒ”÷ADCµÄĶāŠÄ
ĘäÖŠÕżČ·µÄÓŠ£Ø””””£©
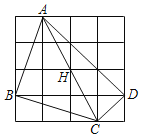
A.1øöB.2øöC.3øöD.4øö
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
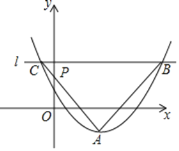
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬Å×ĪļĻßy=![]() -1µÄ¶„µćĪŖA£¬Ö±Ļßl¹żµćP£Ø0£¬m£©ĒŅĘ½ŠŠÓŚxÖį£¬ÓėÅ×ĪļĻß½»ÓŚµćBŗĶµćC£®ČōAB=AC£¬”ĻBAC=90”ć£¬Ōņm=______£®
-1µÄ¶„µćĪŖA£¬Ö±Ļßl¹żµćP£Ø0£¬m£©ĒŅĘ½ŠŠÓŚxÖį£¬ÓėÅ×ĪļĻß½»ÓŚµćBŗĶµćC£®ČōAB=AC£¬”ĻBAC=90”ć£¬Ōņm=______£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ·“±ČĄżŗÆŹż![]() £¬ĻĀĮŠ½įĀŪÖŠ²»ÕżČ·µÄŹĒ£Ø £©
£¬ĻĀĮŠ½įĀŪÖŠ²»ÕżČ·µÄŹĒ£Ø £©
A.Ķ¼Ļó±Ų¾¹żµć ![]() B.
B.![]() Ėę
Ėę![]() µÄŌö“ó¶ųŌö“ó
µÄŌö“ó¶ųŌö“ó
C.Ķ¼ĻóŌŚµŚ¶ž£¬ĖÄĻóĻŽÄŚD.Čō![]() £¬Ōņ
£¬Ōņ![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
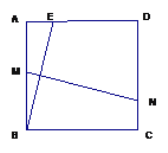
”¾ĢāÄæ”æČēĶ¼£¬ŌŚÕż·½ŠĪABCDÖŠ£¬AB=![]() £¬EŹĒAD±ßÉĻµÄŅ»µć(µćEÓėµćAŗĶµćD²»ÖŲŗĻ)£¬BEµÄ“¹Ö±Ę½·ÖĻß½»ABÓŚµćM£¬½»DCÓŚµćN.
£¬EŹĒAD±ßÉĻµÄŅ»µć(µćEÓėµćAŗĶµćD²»ÖŲŗĻ)£¬BEµÄ“¹Ö±Ę½·ÖĻß½»ABÓŚµćM£¬½»DCÓŚµćN.
(1)Ö¤Ć÷£ŗMN = BE.
(2)ÉčAE=![]() £¬ĖıߊĪADNMµÄĆ껿ĪŖS£¬Š“³öS¹ŲÓŚ
£¬ĖıߊĪADNMµÄĆ껿ĪŖS£¬Š“³öS¹ŲÓŚ![]() µÄŗÆŹż¹ŲĻµŹ½.
µÄŗÆŹż¹ŲĻµŹ½.
(3)µ±AEĪŖŗĪÖµŹ±£¬ĖıߊĪADNMµÄĆ껿×ī“ó£æ×ī“óÖµŹĒ¶ąÉŁ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖµćA£Øx1£¬y1£©”¢B£Øx2£¬y2£©ŌŚ¶ž“ĪŗÆŹży£½x2£«mx£«nµÄĶ¼ĻńÉĻ£¬µ±x1£½1”¢x2£½3Ź±£¬y1£½y2£®
£Ø1£©ČōP£Øa£¬b1£©£¬Q£Ø3£¬b2£©ŹĒŗÆŹżĶ¼ĻóÉĻµÄĮ½µć£¬b1£¾b2£¬ŌņŹµŹżaµÄȔֵ·¶Ī§ŹĒ£Ø £©
A£®a£¼1 B£®a£¾3 C£®a£¼1»ņa£¾3 D£®1£¼a£¼3
£Ø2£©ČōÅ×ĪļĻßÓėxÖįÖ»ÓŠŅ»øö¹«¹²µć£¬Ē󶞓ĪŗÆŹżµÄ±ķ“ļŹ½£®
£Ø3£©Čō¶ŌÓŚČĪŅāŹµŹżx1”¢x2¶¼ÓŠy1£«y2”Ż2£¬ŌņnµÄ·¶Ī§ŹĒ £®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com