
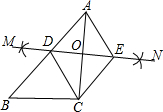
 (2013•宛城区一模)如图,已知△ABC,按如下步骤作图:
(2013•宛城区一模)如图,已知△ABC,按如下步骤作图:| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
| 1 |
| 2 |
|

| AO |
| AC |
| DO |
| CB |
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |


 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•宛城区一模)某校九年级参加了“维护小区周边环境”、“维护繁华街道卫生”、“义务指路”等志愿者活动,如图是根据该校九年级六个班的同学某天“义务指路”总人次所绘制的折线统计图,则关于这六个数据中,下列说法正确的是( )
(2013•宛城区一模)某校九年级参加了“维护小区周边环境”、“维护繁华街道卫生”、“义务指路”等志愿者活动,如图是根据该校九年级六个班的同学某天“义务指路”总人次所绘制的折线统计图,则关于这六个数据中,下列说法正确的是( )查看答案和解析>>
科目:初中数学 来源: 题型:
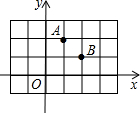 (2013•宛城区一模)点A,B均在由边长为1的相同小正方形组成的网格的格点上,建立平面直角坐标系如图所示,若P是x轴上使得|PA-PB|的值最大的点,Q是y轴上使得QA+QB的值最小的点,则OP+OQ=( )
(2013•宛城区一模)点A,B均在由边长为1的相同小正方形组成的网格的格点上,建立平面直角坐标系如图所示,若P是x轴上使得|PA-PB|的值最大的点,Q是y轴上使得QA+QB的值最小的点,则OP+OQ=( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com