
分析 (1)等式的左边是两个连续奇数的平方差,右边是8的倍数;
(2)根据已知数据得出两连续奇数的平方差的规律即可;
(3)根据(2)中的规律,即可解答.
解答 解:(1)规律:等式的左边是两个连续奇数的平方差,右边是8的倍数;
(2)∵32-12=8=8×1,52-32=16=8×2,72-52=24=8×3,92-72=32=8×4,…
∴设n(n≥1)表示自然数,用关于n的等式表示这个规律为:(2n+1)2-(2n-1)2=8n;
(3)2n+1=2011,
解得:n=1005,
∴20112-20092=8×1005=8040.
故答案为:8040,1005.
点评 本题考查了平方差公式,解决本题的关键是观察等式的规律时,既要分别观察等式的左边和右边,还要注意两边之间的联系.


 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:解答题
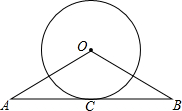 如图,已知直线AB经过⊙O上的点C,且OA=OB,CA=CB.
如图,已知直线AB经过⊙O上的点C,且OA=OB,CA=CB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com