
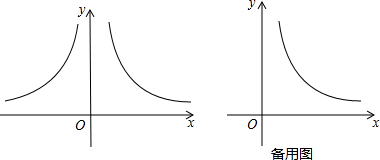
���� ��1�����ݷ���������ϵ��k�ļ�������ó���OAC���OBC�����������ͼ��ɣ�
��2���ֱ���a��b��ʾ��A��B��������꣬�ٸ��ݹ��ɶ����ó�OA2=a2+��$\frac{4}{a}$��2��OB2=b2+��-$\frac{4}{b}$��2����OA=OB���ɵó����ۣ�
��3���������⻭��ͼ�Σ���ֱ��CD�뺯��y=$\frac{4}{x}$��x��0����ͼ��ΪF����a��ʾ��A��C��������꣬�����ɵó�F������꣬���FC�����ֵ�������ɵó����ۣ�
���  �⣺��1����ͼ1��AB��y����C��
�⣺��1����ͼ1��AB��y����C��
��AB��x�ᣬ
��S��OAC=$\frac{1}{2}$��|4|=2��S��OBC=$\frac{1}{2}$��|-4|=2��
��S��OAB=S��OAC+S��OBC=4��
��2������һ���ߵ�A��B�ֱ��ں���y=$\frac{4}{x}$��x��0����y=$\frac{4}{x}$��x��0����ͼ���ϣ�A��B�ĺ�����ֱ�Ϊa��b��
��A��a��$\frac{4}{a}$����B��b��$\frac{4}{b}$����
��OA2=a2+��$\frac{4}{a}$��2��OB2=b2+��-$\frac{4}{b}$��2��
��OA=OBʱ��OA2=OB2
��a2+��$\frac{4}{a}$��2=b2+��-$\frac{4}{b}$��2������4�֣�
�����ã�a2b2��a2-b2��=16��a2-b2����
��a+b��0��a��0��b��0��
��a2-b2��0
��a2b2=16��
��ab=-4��
����������a+b��0��
��AB��x�ƽ��
��B��b��-$\frac{4}{b}$������B��B�����ڹ���ֱ��y=-x�Գƣ�
��B��������$\frac{4}{b}$��-b����
�֡ߵ�A��a��$\frac{4}{a}$����B����$\frac{4}{b}$��-b������y��Գƣ�
��$\frac{4}{a}$=-b���ɴ�ab=-4��
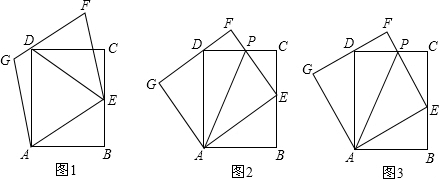
��3����ֱ��CD�뺯��y=$\frac{4}{x}$��x��0����ͼ��ΪF����ͼ2��
��A������Ϊ��a��$\frac{4}{a}$����������ACDE�ı߳�Ϊ3��
��C��������a-3��$\frac{4}{a}$����
��F���������a-3��$\frac{4}{a-3}$����
��FC=$\frac{4}{a-3}$-$\frac{4}{a}$=$\frac{12}{a��a-3��}$��
��a��a-3��=��a-$\frac{3}{2}$��2-$\frac{9}{4}$����a��$\frac{3}{2}$ʱ��a��a-3����ֵ��a��ֵ�����������
��a��a-3������СֵΪ4����4-3��=4��
��FC�����ֵΪ3����FC��DC��
��CD�뺯��y=$\frac{4}{x}$��x��0����ͼ���н��㣮
�ر�أ���a=4ʱ����A������Ϊ��4��1������ʱC��1��1����D��1��4����
��ʱ��D���ں���y=$\frac{4}{x}$��x��0����ͼ���ϣ�
���F���߶�DC�ϣ����Դ��ڻ����4������ʵ��a��CD���뺯��y=$\frac{4}{x}$��x��0����ͼ���н��㣮
���� ���⿼����Ƿ����������ۺ��⣬�漰������������ͼ���ϵ�������ص㡢���������μ������ε����ʣ����κ�������ֵ�����֪ʶ���ѶȽϴ�


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ֱ֪��y=ax+b��������y=ax2+bx����A��B���㣨��A�ڵ�B����ࣩ����C������Ϊ��a��b����
��ֱ֪��y=ax+b��������y=ax2+bx����A��B���㣨��A�ڵ�B����ࣩ����C������Ϊ��a��b�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪��a��b�������϶�Ӧ�ĵ���ͼ��ʾ����|a-b|-$\sqrt{{a}^{2}}$-$\sqrt{{b}^{2}}$=0��
��֪��a��b�������϶�Ӧ�ĵ���ͼ��ʾ����|a-b|-$\sqrt{{a}^{2}}$-$\sqrt{{b}^{2}}$=0���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
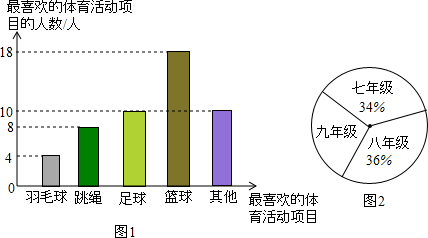
 ��һ�����ǰ���ͼ���ã�ʹ��D����AB�ϣ����EC��AB����ô��DFC�Ķ���Ϊ��������
��һ�����ǰ���ͼ���ã�ʹ��D����AB�ϣ����EC��AB����ô��DFC�Ķ���Ϊ��������| A�� | 45�� | B�� | 50�� | C�� | 60�� | D�� | 75�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ���̵Ľ�����㣬�������� | |
| B�� | ʹ���ĸ��ֵΪ��Ľ������� | |
| C�� | ʹ���ӵ�ֵΪ��Ľ������� | |
| D�� | ֻ��ʹ���з�ĸ��ֵΪ��Ľ�������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\root{3}{3}��1$ | B�� | $\root{3}{-9}��-2$ | C�� | $\root{3}{-7}��-\root{3}{7}$ | D�� | $\root{3}{20}��\sqrt{20}$ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com