
 ��֪������C��y=x2-3x+m��ֱ��l��y=kx��k��0������k=1ʱ��������C��ֱ��lֻ��һ�������㣮
��֪������C��y=x2-3x+m��ֱ��l��y=kx��k��0������k=1ʱ��������C��ֱ��lֻ��һ�������㣮���� ��1����ͼ����һ�����㣬���Ӧ�ķ�������һ��⣬����=0��������㼴�����m��ֵ��
��2�����������ߣ��õ���OAC�ס�OPD��$\frac{OP}{OA}$+$\frac{OP}{OB}$=2��ͬ��$\frac{PD}{AC}$+$\frac{PD}{BE}$=2��AC��BE��x2-��k+3��x+4=0���������ɣ�
��3����S��APQ=S��BPQ�õ�AC+BE=2PD���������̣�k+3��2=16���ɣ�
��� �⣺��1����k=1ʱ��������C��ֱ��lֻ��һ�������㣬
��ֱ��l����ʽΪy=x��
��$\left\{\begin{array}{l}{y={x}^{2}-3x+m}\\{y=x}\end{array}\right.$��
��x2-3x+m=x��
��x2-4x+m=0��
���=16-4m=0��
��m=4��
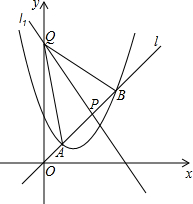
��2����ͼ��
�ֱ����A��P��B��y��Ĵ��ߣ���������ΪC��D��E��
���OAC�ס�OPD��
��$\frac{OP}{OA}=\frac{PD}{AC}$��
ͬ����$\frac{OP}{BO}=\frac{PD}{BE}$��
��$\frac{1}{OA}$+$\frac{1}{OB}$=$\frac{2}{OP}$��
��$\frac{OP}{OA}$+$\frac{OP}{OB}$=2��
��$\frac{PD}{AC}$+$\frac{PD}{BE}$=2��
��$\frac{1}{AC}$+$\frac{1}{BE}$=$\frac{2}{PD}$��
��$\frac{AC+BE}{AC��BE}$=$\frac{2}{PD}$��
�ⷽ����$\left\{\begin{array}{l}{y=kx}\\{y=-3x+b}\end{array}\right.$��
�ã�x=$\frac{b}{k+3}$��
��PD=|$\frac{b}{k+3}$|��
�ɷ�����$\left\{\begin{array}{l}{y=kx}\\{y={x}^{2}-3x+4}\end{array}\right.$��ȥy����x2-��k+3��x+4=0��
��AC��BE������һԪ���η��̵�������
��AC+BE=k+3��AC��BE=4��
�ٵ�b��0ʱ��
��$\frac{k+3}{4}=\frac{2}{\frac{b}{k+3}}$��
���b=8��
�ڵ�b��0ʱ��
��$\frac{k+3}{4}$=-$\frac{2}{\frac{b}{k+3}}$��
��b=-8��
��3�������ڣ��������£�
������ڣ�
��S��APQ=S��BPQʱ����AP=PB��
����PD-AC=BE-PD��
��AC+BE=2PD��
�ɣ�2����֪AC+BE=k+3��PD=$\frac{8}{k+3}$��
��k+3=2��$\frac{8}{k+3}$��
����k+3��2=16��
���k=1����ȥk=-7����
��k=1ʱ��A��B�����غϣ���BQA�����ڣ�
�����ʵ��kʹS��APQ=S��BPQ��
���� �����Ƕ��κ����ۺ��⣬��Ҫ���������������ε����ʺ��ж������������ʣ�һԪ���η��̵ĸ���ϵ���Ĺ�ϵ���Ȿ��Ĺؼ���������ø���ϵ���Ĺ�ϵ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2007 | B�� | 2008 | C�� | 2009 | D�� | 2010 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x��4 | B�� | x��-2��x��4 | C�� | x��-2��x��4 | D�� | x��4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{8}$ | B�� | $\sqrt{12}$ | C�� | $\sqrt{\frac{1}{2}}$ | D�� | $\sqrt{30}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ����һ��ҩƷ���������� | |
| B�� | ��������ȫ����Сѧ���Ŀ����Ķ�ʱ�� | |
| C�� | ����ij������ÿ��Ƿ�Я����Υ����Ʒ | |
| D�� | ����ȫ������ѧ����������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x��3 | B�� | x��3 | C�� | x��3 | D�� | x=3 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com