
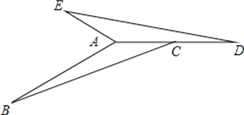
【题目】在△ABC中,∠B+∠ACB=30°,AB=4,△ABC逆时针旋转一定角度后与△ADE重合,且点C恰好成为AD中点,如图
(1)指出旋转中心,并求出旋转角的度数.
(2)求出∠BAE的度数和AE的长.
【答案】(1)150°;(2)2
【解析】分析:(1)先根据三角形内角和计算出∠BAC=150°,然后利用旋转的定义可判断旋转中心为点A,旋转角为150°;(2)根据旋转的性质得到∠DAE=∠BAC=150°,AB=AD=4,AC=AE,利用周角定义可得到∠BAE=60°,然后利用点C为AD中点得到AC=![]() AD=2,于是得到AE=2.
AD=2,于是得到AE=2.
本题解析:
解:(1)在△ABC中,∵∠B+∠ACB=30°, ∴∠BAC=150°,
当△ABC逆时针旋转一定角度后与△ADE重合,
∴旋转中心为点A,∠BAD等于旋转角,即旋转角为150°;
(2)∵△ABC绕点A逆时针旋转150°后与△ADE重合,
∴∠DAE=∠BAC=150°,AB=AD=4,AC=AE, ∴∠BAE=360°-150°-150°=60°,
∵点C为AD中点, ∴AC=![]() AD=2, ∴AE=2.
AD=2, ∴AE=2.


科目:初中数学 来源: 题型:
【题目】如图,铁路上A,B两点相距25 km,C,D为两村庄,DA⊥AB于点A,CB⊥AB于点B,已知DA=16 km,CB=11 km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等,则E站应建在离A站多少km处?

查看答案和解析>>
科目:初中数学 来源: 题型:
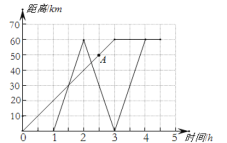
【题目】小南一家到某度假村度假.小南和妈妈坐公交车先出发,爸爸自驾车沿着相同的道路后出发.爸爸到达度假村后,发现忘了东西在家里,于是立即返回家里取,取到东西后又马上驾车前往度假村(取东西的时间忽略不计).如下图是他们离家的距离s(km)与小南离家的时间t(h)的关系图.请根据图回答下列问题:
(1)图中的自变量是_________,因变量是_________,小南家到该度假村的距离是_____km.
(2)小南出发___________小时后爸爸驾车出发,爸爸驾车的平均速度为___________km/h,图中点A表示 .
(3)小南从家到度假村的路途中,当他与爸爸相遇时,离家的距离约是___________km.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数 y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:①a+b+c=0;②b>2a;③ax2+bx+c=0的两根分别为-3和1;④a-2b+c>0.其中正确的命题是( )

A. ①② B. ②③ C. ①③ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某年级380名师生秋游,计划租用7辆客车,现有甲、乙两种型号客车,它们的载客量和租金如表.
甲种客车 | 乙种客车 | |
载客量(座/辆) | 60 | 45 |
租金(元/辆) | 550 | 450 |
(1)设租用甲种客车x辆,租车总费用为y元.求出y(元)与x(辆)之间的函数表达式;
(2)当甲种客车有多少辆时,能保障所有的师生能参加秋游且租车费用最少,最少费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,点D、E分别在AB、AC上,且CE=BC,连接CD,将线段CD绕点C按顺时针方向旋转90°后得到CF,连接EF.
(1)求证:△BDC≌△EFC;
(2)若EF∥CD,求证:∠BDC=90°.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,点
中,点![]() 在
在![]() 边所在直线上(与点
边所在直线上(与点![]() ,
,![]() 不重合),点
不重合),点![]() 在
在![]() 边所在直线上,且
边所在直线上,且![]() ,
,![]() 交
交![]() 边于点
边于点![]() .
.

(1)如图1,若![]() 是等边三角形,点
是等边三角形,点![]() 在
在![]() 边上,过点
边上,过点![]() 作
作![]() 于
于![]() ,试说明:
,试说明:![]() .
.
某同学发现可以由以下两种思路解决此问题:
思路一:过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,如图1
,如图1
因为![]() 是等边三角形,得
是等边三角形,得![]() 是等边三角形
是等边三角形
又由![]() ,得
,得![]()
![]()
再说明![]()
![]()
得出![]() .
.
从而得到结论.
思路二:过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,如图
,如图![]()
①请你在“思路一”中的括号内填写理由;
②根据“思路二”的提示,完整写出说明过程;
(2)如图3,若![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,点
,点![]() 在线段
在线段![]() 的延长线上,过点
的延长线上,过点![]() 作
作![]() 于
于![]() ,试探究
,试探究![]() 与
与![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标中,对称轴平行于y轴的抛物线经过原点O,其顶点坐标为(3,![]() );Rt△ABC的直角边BC在x轴上,直角顶点C的坐标为(
);Rt△ABC的直角边BC在x轴上,直角顶点C的坐标为(![]() ,0),且BC=5,AC=3(如图1).
,0),且BC=5,AC=3(如图1).
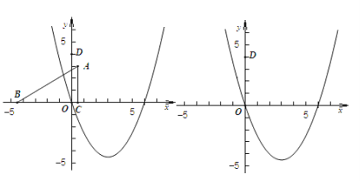
图1 图2
(1)求出该抛物线的解析式;
(2)将Rt△ABC沿x轴向右平移,当点A落在(1)中所求抛物线上时Rt△ABC停止移动.D(0,4)为y轴上一点,设点B的横坐标为m,△DAB的面积为s.
①分别求出点B位于原点左侧、右侧(含原点O)时,s与m之间的函数关系式,并写出相应自变量m的取值范围(可在图1、图2中画出探求);
②当点B位于原点左侧时,是否存在实数m,使得△DAB为直角三角形?若存在,直接写出m的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的正方形网格中,每个小正方形的边长都是1,△ABC的顶点都在正方形网格的格点(网格线的交点)上.
(1)请在如图所示的网格平面内作出平面直角坐标系,使点A坐标为(1,3)点B坐标为(2,1);
(2)请作出△ABC关于y轴对称的△A'B'C',并写出点C'的坐标;
(3)判断△ABC的形状.并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com