
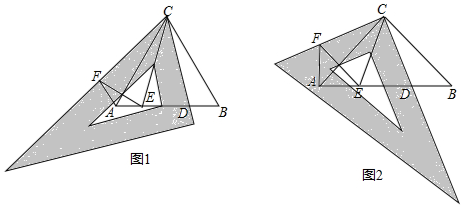
分析 (1)①由等边三角形的性质得出AC=BC,∠BAC=∠B=60°,求出∠ACF=∠BCD,证明△ACF≌△BCD,得出∠CAF=∠B=60°,求出∠EAF=∠BAC+∠CAF=120°;
②证出∠DCE=∠FCE,由SAS证明△DCE≌△FCE,得出DE=EF即可;
(2)①由等腰直角三角形的性质得出AC=BC,∠BAC=∠B=45°,证出∠ACF=∠BCD,由SAS证明△ACF≌△BCD,得出∠CAF=∠B=45°,AF=DB,求出∠EAF=∠BAC+∠CAF=90°;
②证出∠DCE=∠FCE,由SAS证明△DCE≌△FCE,得出DE=EF;在Rt△AEF中,由勾股定理得出AE2+AF2=EF2,即可得出结论.
解答 解:(1)①∵△ABC是等边三角形,
∴AC=BC,∠BAC=∠B=60°,
∵∠DCF=60°,
∴∠ACF=∠BCD,
在△ACF和△BCD中,$\left\{\begin{array}{l}{AC=BC}&{\;}\\{∠ACF=∠BCD}&{\;}\\{CF=CD}&{\;}\end{array}\right.$,
∴△ACF≌△BCD(SAS),
∴∠CAF=∠B=60°,
∴∠EAF=∠BAC+∠CAF=120°;
②DE=EF;理由如下:
∵∠DCF=60°,∠DCE=30°,
∴∠FCE=60°-30°=30°,
∴∠DCE=∠FCE,
在△DCE和△FCE中,$\left\{\begin{array}{l}{CD=CF}&{\;}\\{∠DCE=∠FCE}&{\;}\\{CE=CE}&{\;}\end{array}\right.$,
∴△DCE≌△FCE(SAS),
∴DE=EF;
(2)①∵△ABC是等腰直角三角形,∠ACB=90°,
∴AC=BC,∠BAC=∠B=45°,
∵∠DCF=90°,
∴∠ACF=∠BCD,
在△ACF和△BCD中,$\left\{\begin{array}{l}{AC=BC}&{\;}\\{∠ACF=∠BCD}&{\;}\\{CF=CD}&{\;}\end{array}\right.$,
∴△ACF≌△BCD(SAS),
∴∠CAF=∠B=45°,AF=DB,
∴∠EAF=∠BAC+∠CAF=90°;
②AE2+DB2=DE2,理由如下:
∵∠DCF=90°,∠DCE=45°,
∴∠FCE=90°-45°=45°,
∴∠DCE=∠FCE,
在△DCE和△FCE中,$\left\{\begin{array}{l}{CD=CF}&{\;}\\{∠DCE=∠FCE}&{\;}\\{CE=CE}&{\;}\end{array}\right.$,
∴△DCE≌△FCE(SAS),
∴DE=EF,
在Rt△AEF中,AE2+AF2=EF2,
又∵AF=DB,
∴AE2+DB2=DE2.
点评 本题是几何变换综合题目,考查了旋转的性质、等边三角形的性质、全等三角形的判定与性质、等腰直角三角形的判定与性质、勾股定理等知识;本题综合性强,有一定难度,证明三角形全等是解决问题的关键.


科目:初中数学 来源: 题型:解答题
| 快件到达地 | 首重现付资费(1kg) | 续重现付资费(每kg) |
| 江西 | 10 | 2 |
| 浙江、上海、广东等 | 12 | 4 |
| 北京、天津、山东等 | 15 | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
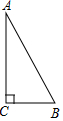 如图,在△ABC中,∠C=90°,AB=10cm,BC=6cm,两只小虫(不计大小)分别从C点出发,小虫1沿CA-AB-BC运动,速度大小为2cm/s,小虫2沿CB-BA-AC运动,速度大小为$\frac{3}{2}$cm/s,相遇后停止.这一过程中两小虫之间的距离y与时间t的关系的大致图象是( )
如图,在△ABC中,∠C=90°,AB=10cm,BC=6cm,两只小虫(不计大小)分别从C点出发,小虫1沿CA-AB-BC运动,速度大小为2cm/s,小虫2沿CB-BA-AC运动,速度大小为$\frac{3}{2}$cm/s,相遇后停止.这一过程中两小虫之间的距离y与时间t的关系的大致图象是( )| A. | 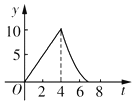 | B. | 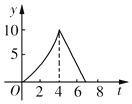 | C. | 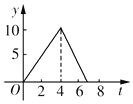 | D. | 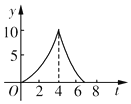 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com