
”¾ĢāÄæ”æČēĶ¼£¬Å×ĪļĻßy=©x2+bx+cµÄĶ¼ĻóÓėxÖį½»ÓŚA(©4£¬0)ŗĶµćBĮ½µć£¬ÓėyÖį½»ÓŚµćC£¬Å×ĪļĻߵĶŌ³ĘÖįŹĒx=©1ÓėxÖį½»ÓŚµćD£®
£Ø1£©ĒóĪļĻßµÄŗÆŹż±ķ“ļŹ½£»
£Ø2£©ČōµćP(m£¬n)ĪŖÅ×ĪļĻßÉĻŅ»µć£¬ĒŅ©4£¼m£¼©1£¬¹żµćP×÷PE”ĪxÖį£¬½»Å×ĪļĻߵĶŌ³ĘÖįx=©1ÓŚµćE£¬×÷PF”ĶxÖįÓŚµćF£¬µĆµ½¾ŲŠĪPEDF£¬Ēó¾ŲŠĪPEDFÖܳ¤µÄ×ī“óÖµ£»
£Ø3£©µćQĪŖÅ×ĪļĻ߶Ō³ĘÖįx=©1ÉĻŅ»µć£¬ŹĒ·ń“ęŌŚµćQ£¬Ź¹ŅŌµćQ£¬B£¬CĪŖ¶„µćµÄČż½ĒŠĪŹĒÖ±½ĒČż½ĒŠĪ£æČō“ęŌŚ£¬ĒėÖ±½ÓŠ“³öµćQµÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®

”¾“š°ø”æ£Ø1£©y=©x2©2x+8£»£Ø2£©µ±m=©![]() Ź±£¬¾ŲŠĪPEDFµÄÖܳ¤ÓŠ×ī“óÖµŹĒ
Ź±£¬¾ŲŠĪPEDFµÄÖܳ¤ÓŠ×ī“óÖµŹĒ![]() £»£Ø3£©“ęŌŚ£¬µćQ (©1£¬
£»£Ø3£©“ęŌŚ£¬µćQ (©1£¬![]() )»ņ(©1£¬©
)»ņ(©1£¬©![]() )»ņ(©1£¬4+
)»ņ(©1£¬4+![]() )»ņ(©1£¬4©
)»ņ(©1£¬4©![]() )£®
)£®
”¾½āĪö”æ
£Ø1£©øł¾ŻÅ×ĪļĻ߶Ō³ĘÖį¹«Ź½ĒóbµÄÖµ£¬Č»ŗó½«Aµć×ų±ź“śČė½āĪöŹ½ĒócµÄÖµ£¬“Ó¶ųĒó½ā£»
£Ø2£©ÉčPµć×ų±źĪŖ(m£¬n)£¬ÓÉĢāŅānØT©m2©2m+8£¬“Ó¶ų±ķŹ¾³ö¾ŲŠĪÖܳ¤µÄŗÆŹż¹ŲĻµŹ½£¬Č»ŗóĄūÓƶž“ĪŗÆŹżµÄŠŌÖŹĒó×īÖµ£»
£Ø3£©ÉčQ(©1£¬y)£¬½įŗĻĶ¼ŠĪÓĆ¹“¹É¶ØĄķ·Ö±š±ķŹ¾³öQB2 =9+y2£¬QC2=1+(y©8)2£¬BC2=68£¬Č»ŗó·Ö”ĻQCB=90”ć£¬”ĻQBC=90”ć£¬”ĻBQC=90”ćČżÖÖĒéæöĮŠ·½³ĢĒó½ā£¬“Ó¶ųČ·¶ØµćQ×ų±ź£®
½ā£ŗ£Ø1£©”ßÅ×ĪļĻßy=©x2+bx+cµÄ¶Ō³ĘÖįŹĒx=©1£¬
”ą©![]() =©1£¬b=©2£¬
=©1£¬b=©2£¬
”ąy=©x2©2x+c£¬
°ŃA(©4£¬0)“śČėµĆ£ŗ©16+8+c=0£¬”ąc=8£¬
”ąĪļĻßµÄŗÆŹż±ķ“ļŹ½ĪŖ£ŗy=©x2©2x+8£»
£Ø2£©”ßµćP(m£¬n)ĪŖÅ×ĪļĻßÉĻŅ»µć£¬ĒŅ©4£¼m£¼©1£¬ČēĶ¼1£¬
 £¬
£¬
”ąnØT©m2©2m+8£®
”ßĖıߊĪPEDFŹĒ¾ŲŠĪ£¬
”ą¾ŲŠĪPEDFµÄÖܳ¤=2PE+2PF
=2(©1©m)+2(©m2©2m+8)
=©2m2©6m+14
=©2(m+![]() )2+
)2+![]() £®
£®
”ß©2£¼0£¬”ąµ±m=©![]() Ź±£¬¾ŲŠĪPEDFµÄÖܳ¤ÓŠ×ī“óÖµŹĒ
Ź±£¬¾ŲŠĪPEDFµÄÖܳ¤ÓŠ×ī“óÖµŹĒ![]() £»
£»
£Ø3£©“ęŌŚµćQ£¬Ź¹ŅŌµćQ£¬B£¬CĪŖ¶„µćµÄČż½ĒŠĪŹĒÖ±½ĒČż½ĒŠĪ£®
”ßµćQĪŖÅ×ĪļĻ߶Ō³ĘÖįx=©1ÉĻŅ»µć£¬”ąÉčQ(©1£¬y)£¬
ÓɶŌ³ĘµĆ£ŗB(2£¬0)£®
”ßC(0£¬8)£¬
”ąQB2=(2+1)2+y2=9+y2£¬QC2=(©1)2+(y©8)2=1+(y©8)2£¬BC2=22+82=4+64=68£¬
·ÖČżÖÖĒéæö£ŗ
¢Łµ±”ĻQCB=90”揱£¬QBŹĒŠ±±ß£¬”ąQB2=QC2+BC2£¬”ą9+y2=1+(y©8)2+68
½āµĆ£ŗy=![]() £¬
£¬
”ąQ(©1£¬![]() )£»
)£»
¢Śµ±”ĻQBC=90”揱£¬QCŹĒŠ±±ß£®
”ßQC2=BC2+QB2£¬”ą1+(y©8)2=68+9+y2£¬
½āµĆ£ŗy=©![]() £¬
£¬
”ąQ(©1£¬©![]() )£»
)£»
¢Ūµ±”ĻBQC=90”揱£¬BCŹĒŠ±±ß£®
”ßBC2=BQ2+QC2£¬”ą68=1+(y©8)2+9+y2£¬
½āµĆ£ŗy=4”Ą![]() £¬”ąQ(©1£¬4+
£¬”ąQ(©1£¬4+![]() )»ņ(©1£¬4©
)»ņ(©1£¬4©![]() )£»
)£»
×ŪÉĻ£¬µćQµÄ×ų±źŹĒ(©1£¬![]() )»ņ(©1£¬©
)»ņ(©1£¬©![]() )»ņ(©1£¬4+
)»ņ(©1£¬4+![]() )»ņ(©1£¬4©
)»ņ(©1£¬4©![]() )£®
)£®


 ĢģĢģĻņÉĻŅ»±¾ŗĆ¾ķĻµĮŠ“š°ø
ĢģĢģĻņÉĻŅ»±¾ŗĆ¾ķĻµĮŠ“š°ø Š”ѧɜ10·ÖÖÓÓ¦ÓĆĢāĻµĮŠ“š°ø
Š”ѧɜ10·ÖÖÓÓ¦ÓĆĢāĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚÕż·½ŠĪ![]() ÖŠ£¬µćEŌŚ±ß
ÖŠ£¬µćEŌŚ±ß![]() ÉĻ£¬½«µćEČʵćDÄꏱÕėŠż×ŖµĆµ½µćF£¬ČōµćFĒ”ŗĆĀäŌŚ±ß
ÉĻ£¬½«µćEČʵćDÄꏱÕėŠż×ŖµĆµ½µćF£¬ČōµćFĒ”ŗĆĀäŌŚ±ß![]() µÄŃÓ³¤ĻßÉĻ£¬Į¬½Ó
µÄŃÓ³¤ĻßÉĻ£¬Į¬½Ó![]() £¬
£¬![]() £¬
£¬![]() £®
£®
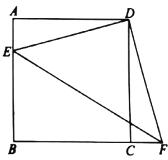
£Ø1£©ÅŠ¶Ļ![]() µÄŠĪד£¬²¢ĖµĆ÷ĄķÓÉ£»
µÄŠĪד£¬²¢ĖµĆ÷ĄķÓÉ£»
£Ø2£©Čō![]() £¬Ōņ
£¬Ōņ![]() µÄĆ껿ĪŖ________£®
µÄĆ껿ĪŖ________£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
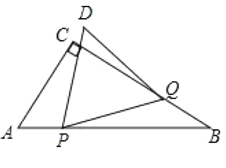
”¾ĢāÄæ”æŌŚ![]() ÖŠ£¬
ÖŠ£¬![]() £¬
£¬![]() £¬
£¬![]() £®¶Æµć
£®¶Æµć![]() ·Ö±š“Óµć
·Ö±š“Óµć![]() Ķ¬Ź±³ö·¢£¬µć
Ķ¬Ź±³ö·¢£¬µć![]() ŅŌĆæĆė1øöµ„Ī»µÄĖŁ¶ČŃŲ
ŅŌĆæĆė1øöµ„Ī»µÄĖŁ¶ČŃŲ![]() ŌČĖŁŌĖ¶Æ£®µć
ŌČĖŁŌĖ¶Æ£®µć![]() ŃŲÕŪĻß
ŃŲÕŪĻß![]() ĻņÖÕµć
ĻņÖÕµć![]() ŌČĖŁŌĖ¶Æ£¬ŌŚ
ŌČĖŁŌĖ¶Æ£¬ŌŚ![]() ÉĻµÄĖŁ¶Č·Ö±šŹĒĆæĆė
ÉĻµÄĖŁ¶Č·Ö±šŹĒĆæĆė![]() øöµ„Ī»”¢ĆæĆė2øöµ„Ī»£®µ±µć
øöµ„Ī»”¢ĆæĆė2øöµ„Ī»£®µ±µć![]() Ķ£Ö¹Ź±£¬µć
Ķ£Ö¹Ź±£¬µć![]() Ņ²ĖęÖ®Ķ£Ö¹ŌĖ¶Æ£®Į¬°“
Ņ²ĖęÖ®Ķ£Ö¹ŌĖ¶Æ£®Į¬°“![]() £¬½«
£¬½«![]() ČĘ×ŵć
ČĘ×ŵć![]() ÄꏱÕėŠż×Ŗ
ÄꏱÕėŠż×Ŗ![]() µĆµ½
µĆµ½![]() £¬Į¬°“
£¬Į¬°“![]() £¬Éčµć
£¬Éčµć![]() µÄŌĖ¶ÆŹ±¼äĪŖ
µÄŌĖ¶ÆŹ±¼äĪŖ![]() £®
£®
£Ø1£©ÓĆŗ¬![]() µÄ“śŹżŹ½±ķŹ¾
µÄ“śŹżŹ½±ķŹ¾![]() µÄ³¤£®
µÄ³¤£®
£Ø2£©µ±µć![]() Óė
Óė![]() µÄ¶„µćÖŲŗĻŹ±£¬Ēó
µÄ¶„µćÖŲŗĻŹ±£¬Ēó![]() µÄ³¤£®
µÄ³¤£®
£Ø3£©Éč![]() µÄĆ껿ĪŖ
µÄĆ껿ĪŖ![]() £¬Ēó
£¬Ēó![]() Óė
Óė![]() Ö®¼äµÄŗÆŹż¹ŲĻµŹ½£®
Ö®¼äµÄŗÆŹż¹ŲĻµŹ½£®
£Ø4£©µć![]() ³ö·¢ŗ󣬵±
³ö·¢ŗ󣬵±![]() Óė
Óė![]() µÄ±ßĖł¼ŠµÄ½Ē±»
µÄ±ßĖł¼ŠµÄ½Ē±»![]() Ę½·ÖŹ±£¬Ö±°“Š“³ö
Ę½·ÖŹ±£¬Ö±°“Š“³ö![]() µÄÖµ£®
µÄÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ2019Äź4ŌĀ18ČÕ£¬ĢØĶåŹ”»ØĮ«ÉĘĻß·¢ÉśĄļŹĻ¼¶![]() µŲÕš£¬¾ČŌ®¶Ó¾ČŌ®Ź±£¬ĄūÓĆÉśĆüĢ½²āŅĒŌŚÄ³½ØÖžĪļ·ĻŠęĻĀ·½Ģ½²āµ½µć
µŲÕš£¬¾ČŌ®¶Ó¾ČŌ®Ź±£¬ĄūÓĆÉśĆüĢ½²āŅĒŌŚÄ³½ØÖžĪļ·ĻŠęĻĀ·½Ģ½²āµ½µć![]() “¦ÓŠÉśĆü¼£Ļó£¬ŅŃÖŖ·ĻŠęŅ»²ąµŲĆęÉĻĮ½Ģ½²āµć
“¦ÓŠÉśĆü¼£Ļó£¬ŅŃÖŖ·ĻŠęŅ»²ąµŲĆęÉĻĮ½Ģ½²āµć![]() Ļą¾ą6Ć×£¬Ģ½²āĻßÓėµŲĆęµÄ¼Š½Ē·Ö±šĪŖ
Ļą¾ą6Ć×£¬Ģ½²āĻßÓėµŲĆęµÄ¼Š½Ē·Ö±šĪŖ![]() ŗĶ
ŗĶ![]() £¬ČēĶ¼ĖłŹ¾£¬ŹŌČ·¶ØÉśĆüĖłŌŚµć
£¬ČēĶ¼ĖłŹ¾£¬ŹŌČ·¶ØÉśĆüĖłŌŚµć![]() µÄÉī¶Č(½į¹ū¾«Č·µ½
µÄÉī¶Č(½į¹ū¾«Č·µ½![]() Ć×£¬²Īæ¼Źż¾Ż
Ć×£¬²Īæ¼Źż¾Ż![]() )
)

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
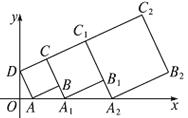
”¾ĢāÄæ”æŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬Õż·½ŠĪABCDµÄĪ»ÖĆČēĶ¼ĖłŹ¾£¬µćAµÄ×ų±źĪŖ(1£¬0)£¬µćDµÄ×ų±źĪŖ(0£¬3)£®ŃÓ³¤CB½»xÖįÓŚµćA1£¬×÷Õż·½ŠĪA1B1C1C£»ŃÓ³¤C1B1½»xÖįÓŚµćA2£¬×÷Õż·½ŠĪA2B2C2C1£¬”£¬°“ÕāŃłµÄ¹ęĀɽųŠŠĻĀČ„£¬µŚ2017øöÕż·½ŠĪµÄĆ껿ĪŖ£Ø £©
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
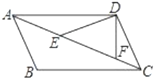
”¾ĢāÄæ”æČēĶ¼£¬![]() ”¢
”¢![]() ŌŚ
ŌŚ![]() µÄ¶Ō½ĒĻß
µÄ¶Ō½ĒĻß![]() ÉĻ£¬
ÉĻ£¬![]() £¬
£¬![]() £¬
£¬![]() £¬Ōņ
£¬Ōņ![]() µÄ“óŠ”ĪŖ£Ø £©£®
µÄ“óŠ”ĪŖ£Ø £©£®
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ¶ž“ĪŗÆŹż![]() µÄĶ¼Ļó¾¹żµć
µÄĶ¼Ļó¾¹żµć![]() .
.
£Ø1£©µ±![]() Ź±£¬Čōµć
Ź±£¬Čōµć![]() ŌŚøƶž“ĪŗÆŹżµÄĶ¼ĻóÉĻ£¬Ēóøƶž“ĪŗÆŹżµÄ±ķ“ļŹ½£»
ŌŚøƶž“ĪŗÆŹżµÄĶ¼ĻóÉĻ£¬Ēóøƶž“ĪŗÆŹżµÄ±ķ“ļŹ½£»
£Ø2£©ŅŃÖŖµć![]() £¬
£¬![]() ŌŚøƶž“ĪŗÆŹżµÄĶ¼ĻóÉĻ£¬Ēó
ŌŚøƶž“ĪŗÆŹżµÄĶ¼ĻóÉĻ£¬Ēó![]() µÄȔֵ·¶Ī§£»
µÄȔֵ·¶Ī§£»
£Ø3£©µ±![]() Ź±£¬Čōøƶž“ĪŗÆŹżµÄĶ¼ĻóÓėÖ±Ļß
Ź±£¬Čōøƶž“ĪŗÆŹżµÄĶ¼ĻóÓėÖ±Ļß![]() ½»ÓŚµć
½»ÓŚµć![]() £¬
£¬![]() £¬ĒŅ
£¬ĒŅ![]() £¬Ēó
£¬Ēó![]() µÄÖµ.
µÄÖµ.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
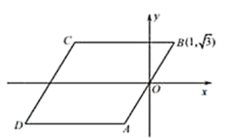
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖĖıߊĪABCDŹĒĮāŠĪ£¬BC”ĪxÖį£¬µćBµÄ×ų±źŹĒ(1£¬![]() )£¬×ų±źŌµćOŹĒABµÄÖŠµć.¶ÆŌ²”ŃPµÄ°ė¾¶ŹĒ
)£¬×ų±źŌµćOŹĒABµÄÖŠµć.¶ÆŌ²”ŃPµÄ°ė¾¶ŹĒ![]() £¬Ō²ŠÄŌŚxÖįÉĻŅĘ¶Æ£¬Čō”ŃPŌŚŌĖ¶Æ¹ż³ĢÖŠÖ»ÓėĮāŠĪABCDµÄŅ»±ßĻąĒŠ£¬ŌņµćPµÄŗį×ų±źm µÄȔֵ·¶Ī§ŹĒ_________£®
£¬Ō²ŠÄŌŚxÖįÉĻŅĘ¶Æ£¬Čō”ŃPŌŚŌĖ¶Æ¹ż³ĢÖŠÖ»ÓėĮāŠĪABCDµÄŅ»±ßĻąĒŠ£¬ŌņµćPµÄŗį×ų±źm µÄȔֵ·¶Ī§ŹĒ_________£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼1£¬ŅŃÖŖÅ×ĪļĻß![]() ¹żµć
¹żµć![]() £®
£®
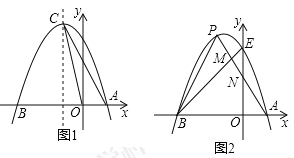
£Ø1£©ĒóÅ×ĪļĻߵĽāĪöŹ½¼°Ę䶄µćCµÄ×ų±ź£»
£Ø2£©ÉčµćDŹĒxÖįÉĻŅ»µć£¬µ±![]() Ź±£¬ĒóµćDµÄ×ų±ź£»
Ź±£¬ĒóµćDµÄ×ų±ź£»
£Ø3£©ČēĶ¼2£®Å×ĪļĻßÓėyÖį½»ÓŚµćE£¬µćPŹĒøĆÅ×ĪļĻßÉĻĪ»ÓŚµŚ¶žĻóĻŽµÄµć£¬Ļ߶ĪPA½»BEÓŚµćM£¬½»yÖįÓŚµćN£¬![]() ŗĶ
ŗĶ![]() µÄĆ껿·Ö±šĪŖ
µÄĆ껿·Ö±šĪŖ![]() £¬Ēó
£¬Ēó![]() µÄ×ī“óÖµ£®
µÄ×ī“óÖµ£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com