
 如图,已知点A(2,3)和点B(0,2),点A在反比例函数y=$\frac{k}{x}$的图象上,作射线AB,再将射线AB绕点A按逆时针方向旋转45°,交反比例函数图象于点C,则点C的坐标为(-1,-6).
如图,已知点A(2,3)和点B(0,2),点A在反比例函数y=$\frac{k}{x}$的图象上,作射线AB,再将射线AB绕点A按逆时针方向旋转45°,交反比例函数图象于点C,则点C的坐标为(-1,-6). 分析 解法1:将点A绕着点B顺时针旋转90°得到点D,连接AD,则△ABD是等腰直角三角形,进而得到点D在射线AC上,根据点A(2,3)和点B(0,2),可得D(1,0),再根据待定系数法求得直线AC的解析式,最后解方程组即可得到点C的坐标;
解法2:先过A作AE⊥x轴于E,以AE为边在AE的左侧作正方形AEFG,交AB于P,根据直线AB的解析式为y=$\frac{1}{2}$x+2,可得PF=$\frac{3}{2}$,将△AGP绕点A逆时针旋转90°得△AEH,构造△ADP≌△ADH,再设DE=x,则DH=DP=x+$\frac{3}{2}$,FD=1+2-x=3-x,在Rt△PDF中,根据PF2+DF2=PD2,可得方程($\frac{3}{2}$)2+(3-x)2=(x+$\frac{3}{2}$)2,进而得到D(1,0),即可得出直线AD的解析式为y=3x-3,最后解方程组即可得到D点坐标.
解答  解法1:如图所示,将点A绕着点B顺时针旋转90°得到点D,连接AD,则△ABD是等腰直角三角形,
解法1:如图所示,将点A绕着点B顺时针旋转90°得到点D,连接AD,则△ABD是等腰直角三角形,
∴∠BAD=45°,
由题可得,∠BAC=45°,
∴点D在射线AC上,
由点A(2,3)和点B(0,2),可得D(1,0),
设AC的解析式为y=ax+b,
把A(2,3),D(1,0)代入,可得
$\left\{\begin{array}{l}{3=2a+b}\\{0=a+b}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=3}\\{b=-3}\end{array}\right.$,
∴直线AC的解析式为y=3x-3,
解方程组$\left\{\begin{array}{l}{y=3x-3}\\{y=\frac{6}{x}}\end{array}\right.$,可得$\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$或$\left\{\begin{array}{l}{x=-1}\\{y=-6}\end{array}\right.$,
∴C(-1,-6),
故答案为:(-1,-6).
解法2:如图所示,过A作AE⊥x轴于E,以AE为边在AE的左侧作正方形AEFG,交AB于P,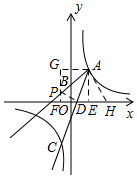
根据点A(2,3)和点B(0,2),可得直线AB的解析式为y=$\frac{1}{2}$x+2,
由A(2,3),可得OF=1,
当x=-1时,y=-$\frac{1}{2}$+2=$\frac{3}{2}$,即P(-1,$\frac{3}{2}$),
∴PF=$\frac{3}{2}$,
将△AGP绕点A逆时针旋转90°得△AEH,则△ADP≌△ADH,
∴PD=HD,PG=EH=$\frac{3}{2}$,
设DE=x,则DH=DP=x+$\frac{3}{2}$,FD=1+2-x=3-x,
Rt△PDF中,PF2+DF2=PD2,
即($\frac{3}{2}$)2+(3-x)2=(x+$\frac{3}{2}$)2,
解得x=1,
∴OD=2-1=1,即D(1,0),
根据点A(2,3)和点D(1,0),可得直线AD的解析式为y=3x-3,
解方程组$\left\{\begin{array}{l}{y=3x-3}\\{y=\frac{6}{x}}\end{array}\right.$,可得$\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$或$\left\{\begin{array}{l}{x=-1}\\{y=-6}\end{array}\right.$,
∴C(-1,-6),
故答案为:(-1,-6).
点评 本题主要考查了反比例函数与一次函数图象交点问题,旋转的性质以及反比例函数图象上点的坐标特征的运用,解决问题的关键是利用45°角,作辅助线构造等腰直角三角形或正方形,依据旋转的性质或勾股定理列方程进行求解.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在一张矩形纸片内,先折出矩形的对角线AC,以AC为折痕折叠AD交BC边于点E,再以AC为折痕折叠BC交AD边于点F,则下列结论不一定正确的是( )
如图,在一张矩形纸片内,先折出矩形的对角线AC,以AC为折痕折叠AD交BC边于点E,再以AC为折痕折叠BC交AD边于点F,则下列结论不一定正确的是( )| A. | AE=CF | B. | AB=AM | C. | AC⊥EF | D. | EF平分∠AEC |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在江苏卫视《最强大脑》节目中,搭载百度大脑的小度机器人以3:1的总战绩,斩获2017年度脑王巅峰对决的晋级资格,人工智能时代已经扑面而来.
在江苏卫视《最强大脑》节目中,搭载百度大脑的小度机器人以3:1的总战绩,斩获2017年度脑王巅峰对决的晋级资格,人工智能时代已经扑面而来.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
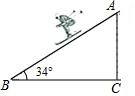 如图,一名滑雪运动员沿着倾斜角为34°的斜坡,从A滑行至B,已知AB=500米,则这名滑雪运动员的高度下降了280米.(参考数据:sin34°≈0.56,cos34°≈0.83,tan34°≈0.67)
如图,一名滑雪运动员沿着倾斜角为34°的斜坡,从A滑行至B,已知AB=500米,则这名滑雪运动员的高度下降了280米.(参考数据:sin34°≈0.56,cos34°≈0.83,tan34°≈0.67)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com