
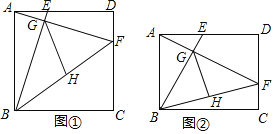
【题目】问题探究:如图①,在正方形![]() 中,点
中,点![]() 在边
在边![]() 上,点
上,点![]() 在边
在边![]() 上,且
上,且![]() .线段
.线段![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 是
是![]() 的中线.
的中线.
(1)求证:![]() ;
;
(2)线段![]() 与
与![]() 之间的数量关系为 .
之间的数量关系为 .
问题拓展:如图②,在矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在边
在边![]() 上,点
上,点![]() 在边
在边![]() 上,且
上,且![]() ,
,![]() ,线段
,线段![]() 与
与![]() 相交于点
相交于点![]() .若
.若![]() 是
是![]() 的中线,则线段
的中线,则线段![]() 的长为 .
的长为 .
【答案】(1)详见解析;(2)![]() ,证明详见解析;问题拓展:
,证明详见解析;问题拓展:![]()
【解析】
(1)由正方形的性质得出∠BAD=∠D=90°,AB=DA,由SAS证明△ABE≌△DAF即可;
(2)由全等三角形的性质得出∠ABE=∠DAF,证出∠BGF=∠ABE+∠BAG=90°,在Rt△BFG中,由直角三角形斜边上的中线性质得出BF=2GH;
问题拓展:由三角函数得出∠ABE=∠DAF,证出∠BGF=90°,在Rt△BFG中,由直角三角形斜边上的中线性质得出BF=2GH,由矩形的性质得出∠C=90°,BC=AD=6,CD=AB=4,得出CF=CD-DF=1,由勾股定理求出BF=![]() ,即可得出GH的长.
,即可得出GH的长.
(1)证明:∵四边形ABCD是正方形,
∴∠BAD=∠D=90°,AB=DA,
在△ABE和△DAF中,
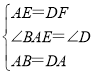 ,
,
∴△ABE≌△DAF(SAS);
(2)解:BF=2GH;理由如下:
∵△ABE≌△DAF,
∴∠ABE=∠DAF,
∵∠DAF+∠BAG=∠BAD=90°,
∴∠ABE+∠BAG=90°,
∴∠BGF=∠ABE+∠BAG=90°,
在Rt△BFG中,GH是边BF的中线,
∴BF=2GH;
问题拓展:
解:∵tan∠ABE=![]() ,tan∠DAF=
,tan∠DAF=![]() ,
,
∴∠ABE=∠DAF,
∵∠DAF+∠BAG=∠BAD=90°,
∴∠ABE+∠BAG=90°,
∴∠AGB=90°,
∴∠BGF=90°,
在Rt△BFG中,GH是边BF的中线,
∴BF=2GH,
∵四边形ABCD是矩形,
∴∠C=90°,BC=AD=6,CD=AB=4,
∴CF=CD-DF=1,
∴BF=![]() ,
,
∴GH=![]() BF=
BF=![]() ;
;
故答案为:![]() .
.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
【题目】某中学决定开展课后服务活动,学校就“你最想开展哪种课后服务项目”问题进行了随机问卷调查,调查分为四个类别:![]() .舞蹈;
.舞蹈;![]() .绘画与书法;
.绘画与书法;![]() .球类;
.球类;![]() .不想参加.现根据调查结果整理并绘制成如下不完整的扇形统计图和条形统计图,请结合图中所给信息解答下列问题:
.不想参加.现根据调查结果整理并绘制成如下不完整的扇形统计图和条形统计图,请结合图中所给信息解答下列问题:
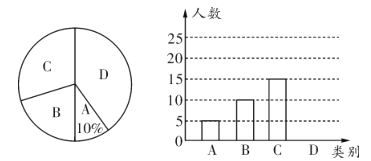
(1)这次统计共抽查了_________名学生,请补全条形统计图;
(2)该校共有600名学生,根据以上信息,请你估计全校学生中想参加![]() 类活动的人数;
类活动的人数;
(3)若甲、乙两名同学,各自从![]() 三个项目中随机选一个参加,请用列表或画树状图的方法求他们选中同一项目的概率.
三个项目中随机选一个参加,请用列表或画树状图的方法求他们选中同一项目的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每到春夏交替时节,雌性杨树会以满天飞絮的方式来传播下一代,漫天飞舞的杨絮易引发皮肤病、呼吸道疾病等,给人们造成困扰,为了解市民对治理杨絮方法的赞同情况,某课题小组随机调查了部分市民(问卷调查表如表所示),并根据调查结果绘制了如下尚不完整的统计图.
治理杨絮一一您选哪一项?(单选)
A.减少杨树新增面积,控制杨树每年的栽种量
B.调整树种结构,逐渐更换现有杨树
C.选育无絮杨品种,并推广种植
D.对雌性杨树注射生物干扰素,避免产生飞絮
E.其他
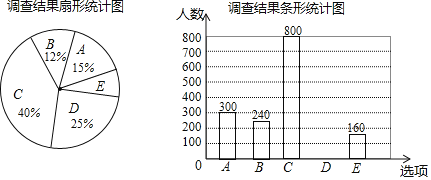
根据以上统计图,解答下列问题:
(1)本次接受调查的市民共有 人;
(2)扇形统计图中,扇形E的圆心角度数是 ;
(3)请补全条形统计图;
(4)若该市约有90万人,请估计赞同“选育无絮杨品种,并推广种植”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校计划选购甲、乙两种图书作为“校园读书节”的奖品.已知甲图书的单价是乙图书单价的1.5倍;用600元单独购买甲种图书比单独购买乙种图书要少10本.
(1)甲、乙两种图书的单价分别为多少元?
(2)若学校计划购买这两种图书总的经费不超过1100元,要求购买的乙种图书是甲种图书的2倍,则甲种图书至多能购买多少本?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,![]() 为矩形
为矩形![]() 的边
的边![]() 上一点,动点
上一点,动点![]() 同时从点
同时从点![]() 出发,点
出发,点![]() 沿折线
沿折线![]() 运动到点
运动到点![]() 时停止,点
时停止,点![]() 沿
沿![]() 运动到点
运动到点![]() 时停止,它们运动的速度都是
时停止,它们运动的速度都是![]() 秒.设
秒.设![]() 同时出发
同时出发![]() 秒时,
秒时,![]() 的面积为
的面积为![]() ,已知
,已知![]() 与
与![]() 的函数关系图象如图2所示.请回答:
的函数关系图象如图2所示.请回答:
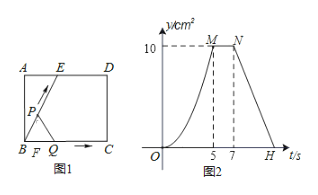
(1)线段![]() 的长为_______cm;
的长为_______cm;
(2)当运动时间![]() 秒时,
秒时,![]() 之间的距离是_______
之间的距离是_______![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的二次函数y=ax2-(2a+2)x+b(a≠0)在x=0和x=6时函数值相等.
(1)求a的值;
(2)若该二次函数的图象与直线y=-2x的一个交点为(2,m),求它的解析式;
(3)在(2)的条件下,直线y=-2x-4与x轴,y轴分别交于A,B,将线段AB向右平移n(n>0)个单位,同时将该二次函数在2≤x≤7的部分向左平移n个单位后得到的图象记为G,请结合图象直接回答,当图象G与平移后的线段有公共点时,n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,二次函数![]() (
(![]() ,
,![]() ,
,![]() 是常数,
是常数,![]() )的图象的一部分与
)的图象的一部分与![]() 轴的交点
轴的交点![]() 在
在![]() 与
与![]() 之间,对称轴为直线
之间,对称轴为直线![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() (
(![]() 为实数);⑤当
为实数);⑤当![]() 时,
时,![]() .其中,正确结论的个数是( )
.其中,正确结论的个数是( )
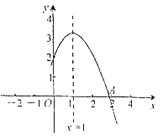
A. 2B. 3C. 4D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了丰富校园文化生活,提高学生的综合素质,促进中学生全面发展,学校开展了多种社团活动.小明喜欢的社团有:合唱社团、足球社团、书法社团、科技社团(分别用字母A,B,C,D依次表示这四个社团),并把这四个字母分别写在四张完全相同的不透明的卡片的正面上,然后将这四张卡片背面朝上洗匀后放在桌面上.
(1)小明从中随机抽取一张卡片是足球社团B的概率是 .
(2)小明先从中随机抽取一张卡片,记录下卡片上的字母后不放回,再从剩余的卡片中随机抽取一张卡片,记录下卡片上的字母.请你用列表法或画树状图法求出小明两次抽取的卡片中有一张是科技社团D的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com