某旅游团一行50人到某旅社住宿,该旅社有三人间、双人间和单人间三种客房,其中三人间每人每晚20元,双人间每人每晚30元,单人间每晚50元.已知该旅行团住满了20间客房,且使总的住宿费用最省.那么这笔最省的住宿费用是________元,所住的三人间、双人间、单人间的间数依次是________.
1150 15、O、5
分析:首先假设该旅行团住三人间x间,双人间y间,单人间z间,总住宿费为a元.根据题目要求列出方程组

.
分别求得y、z用x表示的关系式,且0≤x≤20,0≤y≤20,0≤z≤20,根据y、z用x表示的关系式,确定x的取值范围.将y、z关系式代入60x+60y+50z=a,即得x用a表示的关系式,根据x的取值区间求得a的取值范围,确定a的最小值,此时可求得x的值,代入y、z关于x的关系式,可求得y、z的值.
解答:设该旅行团住三人间x间,双人间y间,单人间z间,总住宿费为a元.
则由题意得

由②-①得 2x+y=30,即y=30-2x ④
由②-①×2得 x-z=10,即z=x-10 ⑤
∵0≤y≤20,即0≤30-2x≤20,解得5≤x≤15 ⑥
同理0≤z≤20,即0≤x-10≤20,解得10≤x≤30 ⑦
由⑥⑦知 10≤x≤15
将④⑤代入③得 a=60x+60(30-2x)+50(x-10)=1300-10x?x=130-
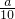
∴10≤

≤15?1200≤a≤1150
∴这笔最省的住宿费用是1150元,此时x=15
再将x的值代入④⑤得 y=0、z=5
故答案为1150,15、O、5.
点评:本题考查三元一次方程组的应用.解决本题的关键是根据题目方程组,求得用x表示的y、z表达式,进而根据0≤x≤20,0≤y≤20,0≤z≤20,求得x的取值范围,进而确定a的取值范围,反过来求得x的取值,y、z的取值.

 .
.
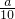
 ≤15?1200≤a≤1150
≤15?1200≤a≤1150

 阅读快车系列答案
阅读快车系列答案