
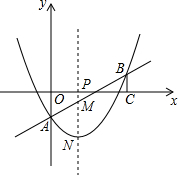
 »ÁÕľňý ĺ£¨Ň◊őÔŌŖy=$\frac{1}{4}$x2+mx+n”Ž÷ĪŌŖy=$\frac{1}{2}$x-2ŌŗĹĽ”ŕĶ„AļÕĶ„B£¨∆š÷–Ķ„A‘ŕy÷Š…Ō£¨ĻżĶ„B◊ųBC°Õx”ň£¨īĻ◊„ő™Ķ„C£®6£¨0£©£ģ
»ÁÕľňý ĺ£¨Ň◊őÔŌŖy=$\frac{1}{4}$x2+mx+n”Ž÷ĪŌŖy=$\frac{1}{2}$x-2ŌŗĹĽ”ŕĶ„AļÕĶ„B£¨∆š÷–Ķ„A‘ŕy÷Š…Ō£¨ĻżĶ„B◊ųBC°Õx”ň£¨īĻ◊„ő™Ķ„C£®6£¨0£©£ģ∑÷őŲ £®1£©Ō»«ůĶ„A°ĘBĶń◊ÝĪÍ£¨ņŻ”√īż∂®ŌĶ ż∑®«ů∂ĢīőļĮ żĶńĹ‚őŲ Ĺ£Ľ
£®2£©łýĺ›Ĺ‚őŲ Ĺ∑÷ĪūĪŪ ĺM°ĘNŃĹĶ„Ķń◊ÝĪÍ£¨”…MN=PM+PNĽÚPN-PMĹÝ––ľ∆ň„£Ľ
£®3£©īś‘ŕ£¨łýĺ›MN=BCŃ–∑Ĺ≥ŐŅ…Ķ√ĹŠ¬Ř£ģ
Ĺ‚īū 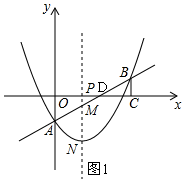 Ĺ‚£ļ£®1£©ĶĪx=6 Ī£¨y=$\frac{1}{2}$°Ń6-2=1£¨
Ĺ‚£ļ£®1£©ĶĪx=6 Ī£¨y=$\frac{1}{2}$°Ń6-2=1£¨
°ŗB£®6£¨1£©£¨
ĶĪx=0 Ī£¨y=-2£¨$\left\{\begin{array}{l}{\frac{1}{4}{x}^{2}+6m+n=1}\\{n=-2}\end{array}\right.$
°ŗA£®0£¨-2£©£¨
į—A£®0£¨-2£©£¨B£®6£¨1£©īķ»ŽŇ◊őÔŌŖĶńĹ‚őŲ Ĺ÷–Ķ√£ļ$\left\{\begin{array}{l}{\frac{1}{4}°Ń{6}^{2}+6m+n=1}\\{n=-2}\end{array}\right.$£¨
Ĺ‚Ķ√£ļ$\left\{\begin{array}{l}{m=-1}\\{n=-2}\end{array}\right.$£¨
°ŗŇ◊őÔŌŖĶńĹ‚őŲ Ĺő™£ļy=$\frac{1}{4}$x2-x-2£Ľ
£®2£©”…Ő‚“‚Ķ√£ļM£®t£¨$\frac{1}{2}$t-2£©£¨N£®t£¨$\frac{1}{4}{t}^{2}$-t-2£©£¨
ĶĪy=0 Ī£¨$\frac{1}{2}$x-2=0£¨
x=4£¨
°ŗD£®4£¨0£©£¨
ĶĪ0°‹t°‹4 Ī£¨»ÁÕľ1£¨PM=2-$\frac{1}{2}$t£¨PN=-$\frac{1}{4}{t}^{2}$+t+2£¨
°ŗMN=PN-PM=-$\frac{1}{4}{t}^{2}$+t+2-2+$\frac{1}{2}$t=-$\frac{1}{4}{t}^{2}$+$\frac{3}{2}$t£¨
ľīs=-$\frac{1}{4}{t}^{2}$+$\frac{3}{2}$t£Ľ
ĶĪ4£ľt°‹6 Ī£¨»ÁÕľ2£¨PM=$\frac{1}{2}$t-2£¨PN=-$\frac{1}{4}{t}^{2}$+t+2£¨
°ŗMN=PM+PN=$\frac{1}{2}$t-2-$\frac{1}{4}{t}^{2}$+t+2=-$\frac{1}{4}{t}^{2}$+$\frac{3}{2}$t£¨
ľīs=-$\frac{1}{4}{t}^{2}$+$\frac{3}{2}$t£Ľ
◊Ř…Ōňý Ų£¨s”ŽtĶńļĮ żĻōŌĶ Ĺő™£ļs=-$\frac{1}{4}{t}^{2}$+$\frac{3}{2}$t£Ľ
£®3£©īś‘ŕ£¨»ÁÕľ3£¨
°ŖPM°Õx÷Š£¨BC°Õx”ň£¨
°ŗPM°őBC£¨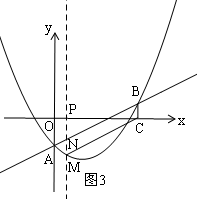
ľīMN°őBC£¨
°ŗĶĪMN=BC Ī£¨ňńĪŖ–őMNCBő™∆Ĺ––ňńĪŖ–ő£¨
ľī-$\frac{1}{4}{t}^{2}$+$\frac{3}{2}$t=1£Ľ
Ĺ‚Ķ√£ļt=3$°ņ\sqrt{5}$£¨
°ŗP£®3+$\sqrt{5}$£¨0£©ĽÚ£®3-$\sqrt{5}$£¨0£©£ģ
Ķ„∆ņ ĪĺŐ‚ «∂ĢīőļĮ żĶń◊ŘļŌŐ‚£¨ń—∂» ÷–£¨Ņľ≤ťŃňņŻ”√īż∂®ŌĶ ż∑®«ů∂ĢīőļĮ żĶńĹ‚őŲ Ĺ°ĘļĮ ż”Ž◊ÝĪÍ÷ŠĶńĹĽĶ„°Ę∆Ĺ––ňńĪŖ–őĶńŇ–∂®£¨‘ŕļĮ żĶń◊ŘļŌŐ‚÷–≥£ņŻ”√ļĮ żĶńĹ‚őŲ ĹĪŪ ĺŌŖ∂őĶń≥§£¨ĪĺŐ‚“≤ «»Áīň£¨Ķę“™◊Ę“‚◊ÝĪÍ”ŽÕľ–őŐōĶ„£ģ



| ńÍľ∂ | łŖ÷–Ņő≥Ő | ńÍľ∂ | ≥ű÷–Ņő≥Ő |
| łŖ“Ľ | łŖ“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű“Ľ | ≥ű“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ∂Ģ | łŖ∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű∂Ģ | ≥ű∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ»ż | łŖ»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű»ż | ≥ű»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° |
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ—°‘ŮŐ‚
| A£ģ | x-5 | B£ģ | 5-x | C£ģ | 5+x | D£ģ | -5-x |
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ—°‘ŮŐ‚
| A£ģ | “Ľīő√ĢĹĪĽÓ∂ĮĶń÷–ĹĪ¬ «l%£¨ń«√ī√Ģ100īőĹĪĪō»ĽĽŠ÷–“ĽīőĹĪ | |
| B£ģ | “ĽłĪ∆ňŅňŇ∆÷–£¨ňś“‚≥ť»°“Ľ’Ň «ļžŐ“K£¨’‚ «Īō»Ľ ¬ľĢ | |
| C£ģ | “ĽłŲ≤ĽÕł√ųĶńīŁ÷–◊į”–3łŲļž«Ú£¨5łŲį◊«Ú£¨»ő“‚√Ģ≥Ų“ĽłŲ«Ú «ļž«ÚĶńłŇ¬ «$\frac{3}{5}$ | |
| D£ģ | Īō»Ľ ¬ľĢĶńłŇ¬ ő™1 |
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ—°‘ŮŐ‚
 ń≥Õ¨—ß≤Ľ–°–ńį—“ĽŅť»żĹ«–ő≤£ŃßīÚňť≥…»żŅť£¨Ō÷“™»•≤£ŃßĶÍŇš÷∆“ĽŅťÕͻꓼ—ýĶń£¨◊Ó °–ńĶńįž∑® «īÝŅť £®°°°°£©
ń≥Õ¨—ß≤Ľ–°–ńį—“ĽŅť»żĹ«–ő≤£ŃßīÚňť≥…»żŅť£¨Ō÷“™»•≤£ŃßĶÍŇš÷∆“ĽŅťÕͻꓼ—ýĶń£¨◊Ó °–ńĶńįž∑® «īÝŅť £®°°°°£©| A£ģ | ĘŔ | B£ģ | Ęŕ | C£ģ | ĘŘ | D£ģ | ĘŔĘŕĘŘ |
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļŐÓŅ’Ő‚
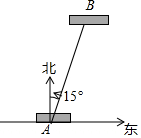 »ÁÕľ£¨“Ľň“ī¨‘ŕAī¶”ŲŌ’ļůŌÚŌŗĺŗ50 ļ£ņÔőĽ”ŕBī¶Ķńĺ»…ķī¨Ī®ĺĮ£ģ”√∑ĹŌÚļÕĺŗņŽ√Ť Ų”ŲŌ’ī¨Ōŗ∂‘”ŕĺ»…ķī¨ĶńőĽ÷√ńŌ∆ęőų15°„£¨50ļ£ņÔ£ģ
»ÁÕľ£¨“Ľň“ī¨‘ŕAī¶”ŲŌ’ļůŌÚŌŗĺŗ50 ļ£ņÔőĽ”ŕBī¶Ķńĺ»…ķī¨Ī®ĺĮ£ģ”√∑ĹŌÚļÕĺŗņŽ√Ť Ų”ŲŌ’ī¨Ōŗ∂‘”ŕĺ»…ķī¨ĶńőĽ÷√ńŌ∆ęőų15°„£¨50ļ£ņÔ£ģ≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļŐÓŅ’Ő‚
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļŐÓŅ’Ő‚
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļĹ‚īūŐ‚
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļĹ‚īūŐ‚

| a-1 | a |
| a+6 | a+7 |
≤ťŅīīūįłļÕĹ‚őŲ>>
įŔ∂»÷¬–Ň - Ń∑Ōį≤ŠŃ–ĪŪ - ‘Ő‚Ń–ĪŪ
ļĢĪĪ °Ľ•Ń™ÕÝő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®∆ĹŐ® | ÕÝ…Ō”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | ĶÁ–Ň’©∆≠ĺŔĪ®◊®«Ý | …śņķ ∑–ťőř÷ų“Ś”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | …ś∆ů«÷»®ĺŔĪ®◊®«Ý
ő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®ĶÁĽį£ļ027-86699610 ĺŔĪ®” Ōš£ļ58377363@163.com