
【题目】如图,在 △ABC和 △ADE中,∠BAD=∠CAE, ∠ABC=∠ADE.
(1)写出图中两对相似三角形(不得添加字母和线);
(2)请证明你写出的两对相似三角形.

【答案】(1)见解析;(2)见解析.
【解析】
(1)△ABC∽△ADE,△ABD∽△ACE;
(2)∠BAD=∠CAE,在此等式两边各加∠DAC,可证∠BAC=∠DAE,再结合已知中的∠ABC=∠ADE,可证△ABC∽△ADE;利用△ABC∽△ADE,可得AB:AD=AC:AE,再结合∠BAD=∠CAE,也可证△BAD∽△CAE.
(1)△ABC∽△ADE,△ABD∽△ACE;
(2)①证△ABC∽△ADE,
∵∠BAD=∠CAE,
∠BAD+∠DAC=∠CAE+∠DAC,
即∠BAC=∠DAE.
又∵∠ABC=∠ADE,
∴△ABC∽△ADE.
②证△ABD∽△ACE,
∵△ABC∽△ADE,
∴![]() .
.
又∵∠BAD=∠CAE,
∴△ABD∽△ACE.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:初中数学 来源: 题型:
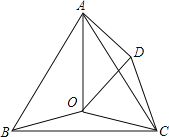
【题目】如图,O是等边三角形ABC内一点,∠AOB=110°,∠BOC=m°,D是△ABC外一点,且△ADC≌△BOC,连接OD.当m为_____时,△AOD是等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明与同学们在数学动手实践操作活动中,将锐角为![]() 的直角三角板MPN的一个锐角顶点P与正方形ABCD的顶点A重合,正方形ABCD固定不动,然后将三角板绕着点A旋转,
的直角三角板MPN的一个锐角顶点P与正方形ABCD的顶点A重合,正方形ABCD固定不动,然后将三角板绕着点A旋转,![]() 的两边分别与正方形的边BC、DC或其延长线相交于点E、F,连结EF.
的两边分别与正方形的边BC、DC或其延长线相交于点E、F,连结EF.
(探究发现)
![]() 在三角板旋转过程中,当
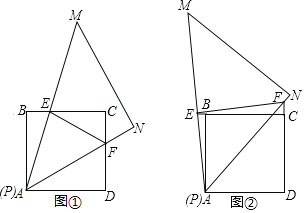
在三角板旋转过程中,当![]() 的两边分别与正方形的边CB、DC相交时,如图
的两边分别与正方形的边CB、DC相交时,如图![]() 所示,请直接写出线段BE、DF、EF满足的数量关系:______.
所示,请直接写出线段BE、DF、EF满足的数量关系:______.
(拓展思考)
![]() 在三角板旋转过程中,当
在三角板旋转过程中,当![]() 的两边分别与正方形的边CB、DC的延长线相交时,如图
的两边分别与正方形的边CB、DC的延长线相交时,如图![]() 所示,则线段BE、DF、EF又将满足怎样的数量关系:______,并证明你的结论;
所示,则线段BE、DF、EF又将满足怎样的数量关系:______,并证明你的结论;
(创新应用)
![]() 若正方形的边长为4,在三角板旋转过程中,当
若正方形的边长为4,在三角板旋转过程中,当![]() 的一边恰好经过BC边的中点时,试求线段EF的长.
的一边恰好经过BC边的中点时,试求线段EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)一个不透明的盒中装有若干个除颜色外都相同的红球与黄球.在这个口袋中先放入2个白球,再进行摸球试验,摸球试验的要求:先搅拌均匀,每次摸出一个球,记录颜色后放回盒中,再继续摸球,全班一共做了400次这样的摸球试验.如果知道摸出白球的频数是40,你能估计在未放入白球前,袋中原来共有多少个小球吗?
(2)提出问题:一个不透明的盒中装有若干个只有颜色不一样的红球与黄球,怎样估算不同颜色球的数量?
活动操作:先从盒中摸出8个球,画上记号放回盒中.再进行摸球试验,摸球试验的要求:先搅拌均匀,每次摸出一个球,记录颜色、是否有记号,放回盒中,再继续摸球、记录、放回袋中.
统计结果:摸球试验活动一共做了50次,统计结果如下表:
球的类别 | 无记号 | 有记号 | ||
红色 | 黄色 | 红色 | 黄色 | |
摸到的次数 | 18 | 28 | 2 | 2 |
由上述的摸球试验推算:
①盒中红球、黄球各占总球数的百分比分别是多少?
②盒中有红球多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
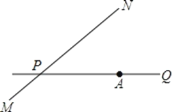
【题目】如图,公路 MN 和公路 PQ 在点 P 处交会,且∠QPN=30°.点 A 处有一所中学,AP=160m,一辆拖拉机从 P 沿公路 MN 前行,假设拖拉机行驶时周围 100m 以内会受到噪声影响,那么该所中学是否会受到噪声影响,请说明理由,若受影响,已知拖拉机的速度为 18km/h,那么学校受影响的时间为多长?
查看答案和解析>>
科目:初中数学 来源: 题型:
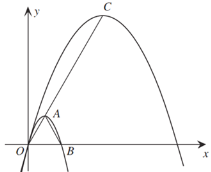
【题目】如图,抛物线C1:![]() 的顶点为A,与x轴的正半轴交于点B.
的顶点为A,与x轴的正半轴交于点B.
(1)请直接写出A、B两点的坐标,A ,B .
(2)将抛物线C1上的点的横坐标和纵坐标都扩大到原来的2倍,求变换后得到的抛物线的解析式;
(3)将抛物线C1上的点(x,y)变为(kx,ky)(|k|>1),变换后得到的抛物线记作C2.抛物线C2的顶点为C,点P在抛物线C2上,满足S△PAC=S△ABC,且∠ACP=90°.
①当k>1时,求k的值;
②当k<-1时,请你直接写出k的值,不必说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个木制的棱长为3的正方体的表面涂上颜色,将它的棱三等分,然后从等分点把正方体锯开,得到27个棱长为l的小正方体,将这些小正方体充分混合后,装入口袋,从这个口袋中任意取出一个小正方体,则这个小正方体的表面恰好涂有两面颜色的概率是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】黄岩某校搬迁后,需要增加教师和学生的寝室数量,寝室有三类,分别为单人间(供一个人住宿),双人间(供两个人住宿),四人间(供四个人住宿).因实际需要,单人间的数量在20至30之间(包括20和30),且四人间的数量是双人间的5倍.
(1)若2018年学校寝室数为64个,以后逐年增加,预计2020年寝室数达到121个,求2018至2020年寝室数量的年平均增长率;
(2)若三类不同的寝室的总数为121个,则最多可供多少师生住宿?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com