
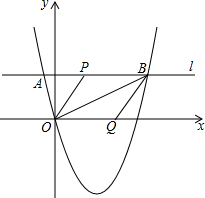
 如图,抛物线y=ax2+3(a-1)x(a>0)经过点A(-3,m),过点A作直线l平行于x轴与抛物线交于另一点B,在x轴上取点Q,连接BQ,使得∠QBO=∠ABO,过点O作OP平行BQ交l于点P,若AP=$\frac{1}{2}$AB,则a的值为$\frac{1}{9}$.
如图,抛物线y=ax2+3(a-1)x(a>0)经过点A(-3,m),过点A作直线l平行于x轴与抛物线交于另一点B,在x轴上取点Q,连接BQ,使得∠QBO=∠ABO,过点O作OP平行BQ交l于点P,若AP=$\frac{1}{2}$AB,则a的值为$\frac{1}{9}$. 分析 首先证明AO⊥OB,把点A代入抛物线解析式得到m=9,利用相似三角形性质求出BK,求出点B坐标即可解决问题.
解答 解:如图连接OA,PQ.
∵PB∥OQ,OP∥BQ,
∴四边形OPBQ是平行四边形,
∵∠OBQ=∠ABO=∠BOQ,
∴QB=QO,
∴四边形OPBQ是菱形,
∴OQ=PB,PQ⊥OB,
∵AP=PB,
∴AP=OQ,AP∥OQ,
∴四边形APQO是平行四边形,
∴AO∥PQ,
∴AO⊥OB,∠AOB=90°,
把点A(-3,m)代入抛物线解析式,m=9a-9(a-1),
∴m=9,
由△AOK∽△OBK得到,OK2=AK•KB,
∴KB=27,
∴点B坐标(27,9)代入抛物线得到:9=272×a+3×27(a-1),
解得a=$\frac{1}{9}$.
故答案为$\frac{1}{9}$.
点评 本题考查二次函数的性质、相似三角形的判定和性质、菱形的判定和性质、平行四边形的判定和性质等知识,解题的关键是利用待定系数法求出m的值,得到点B坐标,属于中考常考题型.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:选择题
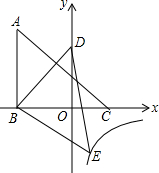 如图,△ABC的三个顶点的坐标分别为A(-3,5),B(-3,0),C(2,0),将△ABC绕点B顺时针旋转一定的角度后得到△DBE,且使点D落在y轴上,与此同时顶点E恰好落在y=$\frac{k}{x}$的图象上,则k的值为( )
如图,△ABC的三个顶点的坐标分别为A(-3,5),B(-3,0),C(2,0),将△ABC绕点B顺时针旋转一定的角度后得到△DBE,且使点D落在y轴上,与此同时顶点E恰好落在y=$\frac{k}{x}$的图象上,则k的值为( )| A. | -3 | B. | -4 | C. | -5 | D. | -3$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
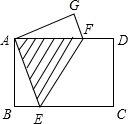 如图,矩形纸片ABCD中,AB=3cm,BC=4cm,现将A、C重合,使纸片折叠压平,设折痕为EF,试确定重叠部分的△AEF的面积是$\frac{25}{16}$.
如图,矩形纸片ABCD中,AB=3cm,BC=4cm,现将A、C重合,使纸片折叠压平,设折痕为EF,试确定重叠部分的△AEF的面积是$\frac{25}{16}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,正方形ABCD边长为4个单位,两动点P、Q分别从点A、B处,以1单位/s、2单位/s的速度逆时针沿边移动.记移动的时间为x(s),△PBQ面积为y(平方单位),当点Q移动一周又回到点B终止,则y与x的函数关系图象为( )
如图,正方形ABCD边长为4个单位,两动点P、Q分别从点A、B处,以1单位/s、2单位/s的速度逆时针沿边移动.记移动的时间为x(s),△PBQ面积为y(平方单位),当点Q移动一周又回到点B终止,则y与x的函数关系图象为( )| A. | 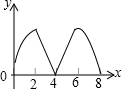 | B. | 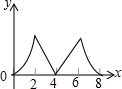 | C. |  | D. | 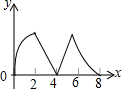 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 8 | B. | 5 | C. | 2 | D. | 0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com